题目内容
14．已知在△ABC中，b=2，c=$\sqrt{3}$，c=60°，则∠A=（ ）| A． | 30° | B． | 60° | C． | 30°或150° | D． | 60°或120° |
分析 由已知及正弦定理可得：sinB=$\frac{bsinC}{c}$=1，又B为三角形内角，解得B=90°，利用三角形内角和定理即可求得A的值．
解答 解：∵b=2，c=$\sqrt{3}$，c=60°，
∴由正弦定理可得：sinB=$\frac{bsinC}{c}$=$\frac{2×sin60°}{\sqrt{3}}$=1，B为三角形内角，解得B=90°，
∴A=180°-B-C=30°．
故选：A．
点评 本题主要考查了正弦定理，三角形内角和定理的应用，属于基础题．
练习册系列答案
相关题目
9．已知△ABC三个内角A，B，C的对边分别为a，b，c，且A，B，C成等差数列，若△ABC的面积为2$\sqrt{3}$，则a+2c的最小值为（ ）
| A． | 8 | B． | 6 | C． | 4 | D． | $\sqrt{6}$ |
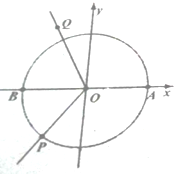如图，角α的顶点在坐标原点O，始边在x轴的正半轴，终边与单位圆交于点P（-$\frac{3}{5}$，sinα），且$π＜α＜\frac{3π}{2}$，角β的顶点在原点O，始边在x轴正半轴，终边OQ落在第二象限，且tanβ=-2，