题目内容
函数 是定义在R上的奇函数,下列结论中,不正确的是
是定义在R上的奇函数,下列结论中,不正确的是
A. | B. |
C. | D. |
D
解析试题分析:解:∵f(x)是定义在R上的奇函数,∴f(-x)=-f(x)且f(0)=0,可变形为:f(-x)+f(x)=0,f(-x)-f(x)=-2f(x),f(x)•f(-x)≤0,而由f(0)=0,由知D不正确.故选D
考点:函数奇偶性
点评:本题主要考查函数奇偶性模型的各种变形,数学建模,用模,解模的意识要加强,每一个概念,定理,公式都要从模型的意识入手.

练习册系列答案
相关题目
函数 的零点所在区间为
的零点所在区间为
A. | B. | C. | D. |
若a>l,设函数f(x)=ax+x -4的零点为m,函数g(x)= logax+x-4的零点为n,则 的最小值为
的最小值为
| A.1 | B.2 | C.4 | D.8 |
函数f(x)=x- 的零点是( )
的零点是( )
| A.0 | B.1 | C.2 | D.无数个 |
定义在 上的函数
上的函数 ,满足
,满足 ,
,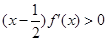 ,若
,若 且
且 ,则有( ).
,则有( ).
A. | B. | C. | D.不能确定 |
如下图是函数 的大致图象,则
的大致图象,则 等于
等于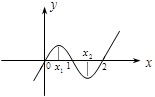
A.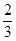 | B. |
C. | D. |

 的一个零点所在的区
的一个零点所在的区 ,则
,则 的值为( )
的值为( )


 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数 的图象是( ).
的图象是( ).
