题目内容
某学生从家里去学校上学，骑自行车一段时间，因自行车爆胎，后来推车步行，下图中横轴表示出发后的时间，纵轴表示该生离学校的距离，则较符合该学生走法的图是（ ）
D
解析试题分析：利用函数的单调性排除两项，再利用曲线的斜率反映行进速度的特点选出正确结果. 解：随着时间的增加，距学校的距离在减小，即函数图象应为减函数，排除A、C,曲线的斜率反映行进的速度，斜率的绝对值越大速度越大，步行后速度变小，故排除B,故选D
考点：函数单调性
点评：本题考查了函数单调性，函数图象的倾斜角的实际意义，排除法解选择题
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
函数
的图象如图所示，则
的解析式可能是 （ ） 
A． | B． |
C． | D． |
函数
的定义域是 （ ）
A． | B． |
C． | D． |
已知
是定义在R上的奇函数，若对于x≥0，都有f(x+2)=，且
当
时，
，则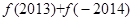
=（ ）
| A．1-e | B．e-1 | C．-l-e | D．e+l |
下列函数中，在区间（0，1）上是增函数的是（ ）
A． | B． | C． | D． |
下列各组函数中，表示同一函数的是( )
A． | B． |
C． | D． |
函数
是定义在R上的奇函数，下列结论中，不正确的是
A． | B． |
C． | D． |
已知函数
的定义域为
,部分对应值如下表。的导函数
的图像如图所示。
 |  | 0 |  |  |  |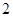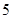
|  | |  | | |
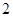下列关于函数
的命题：①函数
在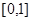
上是减函数；②如果当
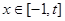时，最大值是，那么
的最大值为；③函数
有个零点，则
；④已知
是
的一个单调递减区间，则
的最大值为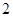。其中真命题的个数是（ ）
A、4个 B、3个 C、2个 D、1个
若函数
在
是增函数，则a的取值范围是（ ）
A． | B． | C． | D． |