Question

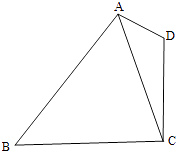
【题目】如图，在平面四边形ABCD中，AD=1，CD=2，AC= ．
（1）求cos∠CAD的值；
（2）若cos∠BAD=﹣ ，sin∠CBA= ，求BC的长．

Answer 1

【答案】
（1）解：cos∠CAD= = =
（2）解：∵cos∠BAD=﹣ ，

∴sin∠BAD= = ，

∵cos∠CAD= ，

∴sin∠CAD= =

∴sin∠BAC=sin（∠BAD﹣∠CAD）=sin∠BADcos∠CAD﹣cos∠BADsin∠CAD= × + × = ，

∴由正弦定理知 = ，

∴BC= sin∠BAC= × =3

【解析】（1）利用余弦定理，利用已知条件求得cos∠CAD的值．（2）根据cos∠CAD，cos∠BAD的值分别，求得sin∠BAD和sin∠CAD，进而利用两角和公式求得sin∠BAC的值，最后利用正弦定理求得BC．