题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,其焦距为
,其焦距为![]() ,点E为椭圆的上顶点,且
,点E为椭圆的上顶点,且![]() .
.
(1)求椭圆C的方程;
(2)设圆![]() 的切线l交椭圆C于A,B两点(O为坐标原点),求证
的切线l交椭圆C于A,B两点(O为坐标原点),求证![]() ;
;
(3)在(2)的条件下,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)由焦距可求出![]() ,由
,由![]() ,可求出
,可求出![]() ,
,![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)当切线与![]() 轴垂直时,求出焦点坐标,进而证得
轴垂直时,求出焦点坐标,进而证得![]() ;当切线与
;当切线与![]() 轴不垂直时,设切线方程,联立切线方程与椭圆方程,列韦达定理,利用
轴不垂直时,设切线方程,联立切线方程与椭圆方程,列韦达定理,利用![]() ,即可证明;
,即可证明;
(3)当切线与![]() 轴垂直时,
轴垂直时,![]() ;当切线与
;当切线与![]() 轴不垂直时,由
轴不垂直时,由![]() 、韦达定理以及弦长公式,可求出
、韦达定理以及弦长公式,可求出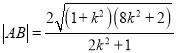 ,借助基本不等式即可求出
,借助基本不等式即可求出![]() 的最大值.
的最大值.
(1)由题意知![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]()
![]() ,
,
椭圆![]() 的方程为
的方程为![]() .
.
(2)(ⅰ)当切线与![]() 轴垂直时,
轴垂直时,
交点坐标为![]() ,
,![]() ,
,![]() ;
;
(ⅱ)当切线与![]() 轴不垂直时,
轴不垂直时,
设切线为![]() ,
,![]() ,
,![]() ,
,
由圆心到直线距离为![]() ,
,![]()
![]() ,
,
联立直线方程与椭圆方程,得![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
(3)当切线与![]() 轴垂直时,
轴垂直时,![]() ;
;
当切线与![]() 轴不垂直时,由(2)知
轴不垂直时,由(2)知![]() ,
,![]() ,
,
∵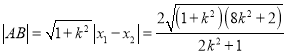 ,
,
令![]() ,则
,则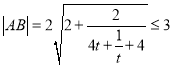 ,
,
当且仅当![]() 时等号成立,
时等号成立,![]()
![]() .
.
综上所述,![]() 的最大值为
的最大值为![]() .
.

【题目】2020年春节期间,全国人民都在抗击“新型冠状病毒肺炎”的斗争中.当时武汉多家医院的医用防护物资库存不足,某医院甚至面临断货危机,南昌某生产商现有一批库存的医用防护物资,得知消息后,立即决定无偿捐赠这批医用防护物资,需要用A、B两辆汽车把物资从南昌紧急运至武汉.已知从南昌到武汉有两条合适路线选择,且选择两条路线所用的时间互不影响.据调查统计2000辆汽车,通过这两条路线从南昌到武汉所用时间的频数分布表如下:
所用的时间(单位:小时) |
|
|
|
|
路线1的频数 | 200 | 400 | 200 | 200 |
路线2的频数 | 100 | 400 | 400 | 100 |
假设汽车A只能在约定交货时间的前5小时出发,汽车B只能在约定交货时间的前6小时出发(将频率视为概率).为最大可能在约定时间送达这批物资,来确定这两车的路线.
(1)汽车A和汽车B应如何选择各自的路线.
(2)若路线1、路线2的“一次性费用”分别为3.2万元、1.6万元,且每车医用物资生产成本为40万元(其他费用忽略不计),以上费用均由生产商承担,作为援助金额的一部分.根据这两辆车到达时间分别计分,具体规则如下(已知两辆车到达时间相互独立,互不影响):
到达时间与约定时间的差x(单位:小时) |
|
|
|
该车得分 | 0 | 1 | 2 |
生产商准备根据运输车得分情况给出现金排款,两车得分和为0,捐款40万元,两车得分和每增加1分,捐款增加20万元,若汽车A、B用(1)中所选的路线运输物资,记该生产商在此次援助活动中援助总额为Y(万元),求随机变量Y的期望值,(援助总额![]() 一次性费用
一次性费用![]() 生产成本
生产成本![]() 现金捐款总额)
现金捐款总额)