题目内容
 选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且BD=
选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且BD=| 1 |
| 3 |
| 1 |
| 3 |
求证:
(1)P,D,C,E四点共圆;
(2)AP⊥CP.
分析:(1)利用边角边公理,证出△ABD≌△BCE,得∠ADB=∠BEC,再用平角的定义与等量代换,得出∠PDC+∠BEC=π,所以四边形PDCE是圆内接四边形,即P,D,C,E四点共圆;
(2)连接DE,在△CDE中利用余弦定理和勾股定理的逆定理,得到∠CED=90°,再结合(1)四边形PDCE是圆内接四边形得到∠DPC=∠CED=90°,可证出AP⊥CP.
(2)连接DE,在△CDE中利用余弦定理和勾股定理的逆定理,得到∠CED=90°,再结合(1)四边形PDCE是圆内接四边形得到∠DPC=∠CED=90°,可证出AP⊥CP.
解答:解:(1)∵正△ABC中,BD=
BC,CE=
CA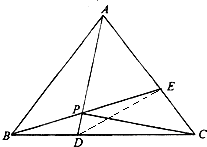
∴BD=CE,AB=BC且∠ABD=∠BCE=60°
∴△ABD≌△BCE,得∠ADB=∠BEC
∵∠PDC+∠ADB=π,
∴∠PDC+∠BEC=π,得四边形PDCE的对角互补
∴四边形PDCE是圆内接四边形,即P,D,C,E四点共圆;---(5分)
(2)如图,连接DE,
∵在△CDE中,CD=2CE,∠DCE=60°,
∴由余弦定理,得DE2=CD2+CE2-2CD•CEcos60°=3CE2
由此可得CE2+DE2=4CE2=CD2,所以∠CED=90°
∵P,D,C,E四点共圆
∴∠DPC=∠CED=90°,得AP⊥CP
| 1 |
| 3 |
| 1 |
| 3 |

∴BD=CE,AB=BC且∠ABD=∠BCE=60°
∴△ABD≌△BCE,得∠ADB=∠BEC
∵∠PDC+∠ADB=π,
∴∠PDC+∠BEC=π,得四边形PDCE的对角互补
∴四边形PDCE是圆内接四边形,即P,D,C,E四点共圆;---(5分)
(2)如图,连接DE,
∵在△CDE中,CD=2CE,∠DCE=60°,
∴由余弦定理,得DE2=CD2+CE2-2CD•CEcos60°=3CE2
由此可得CE2+DE2=4CE2=CD2,所以∠CED=90°
∵P,D,C,E四点共圆
∴∠DPC=∠CED=90°,得AP⊥CP
点评:本题给出正三角形的两个三等分点,得到全等三角形,求证四点共圆并证明两直线垂直,着重考查了三角形全等的判定、圆內接多边形的性质与判定和余弦定理等知识,属于中档题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲