题目内容
如图所示,在正方体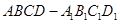 中,点
中,点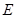 是棱
是棱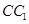 上的一个动点,平面
上的一个动点,平面 交棱
交棱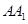 于点
于点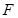 .给出下列四个结论:
.给出下列四个结论:
①存在点 ,使得
,使得 //平面
//平面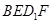 ;
;
②存在点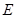 ,使得
,使得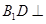 平面
平面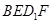 ;
;
③对于任意的点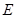 ,平面
,平面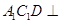 平面
平面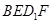 ;
;
④对于任意的点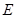 ,四棱锥
,四棱锥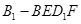 的体积均不变.
的体积均不变.
其中,所有正确结论的序号是___________.
①③④
解析试题分析:当点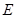 为
为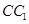 的中点时,由对称性可知
的中点时,由对称性可知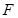 也是
也是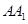 的中点,此时
的中点,此时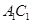 //
//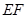 ,因为
,因为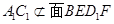 ,
,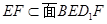 ,所以
,所以 //
//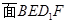 ,故①正确;
,故①正确;
假设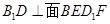 ,因为
,因为 ,所以
,所以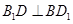 。所以四边形
。所以四边形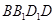 为菱形或正方形,即
为菱形或正方形,即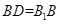 。因为
。因为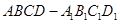 为正方体所以
为正方体所以 。所以假设不成立。故②不正确。
。所以假设不成立。故②不正确。
因为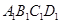 为正方形,所以
为正方形,所以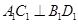 ,因为
,因为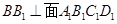 ,
,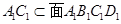 ,所以
,所以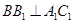 ,因为
,因为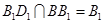 ,所以
,所以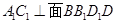 。因为
。因为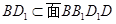 ,所以
,所以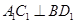 。同理可证
。同理可证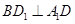 ,因为
,因为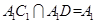 ,所以
,所以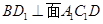 ,因为
,因为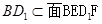 ,所以
,所以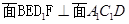 。故③正确。
。故③正确。
设正方体边长为 ,则
,则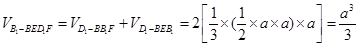 。故④正确。
。故④正确。
综上可得正确的是①③④。
考点:1线线平行、线面平行;2线线垂直、线面垂直;3棱锥的体积。

练习册系列答案
相关题目
 中,
中,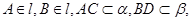 且
且 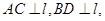 若
若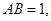
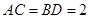 ,
, 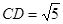 , 则二面角
, 则二面角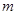 ,
,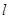 和平面
和平面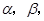 且
且 ,给出下列四个命题:
,给出下列四个命题: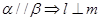 ②
②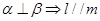 ③
③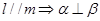 ④
④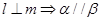
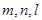 是互不重合的直线,
是互不重合的直线,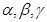 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题: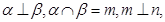 则
则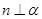 或
或 ;
;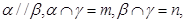 则
则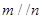 ;
;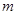 不垂直于
不垂直于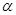 ,则
,则 且
且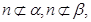 则
则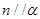
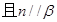 ;
;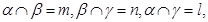 且
且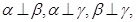 则
则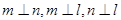 .
. 中,
中,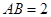 ,点
,点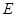 为
为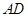 的中点,点
的中点,点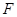 在
在 上,若
上,若 ,则线段
,则线段 的长度等于______.
的长度等于______.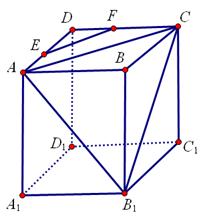
 、
、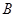 为正方体的两个顶点,
为正方体的两个顶点, 、
、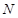 、
、 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出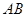 //平面
//平面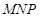 的图形的序号是 .
的图形的序号是 .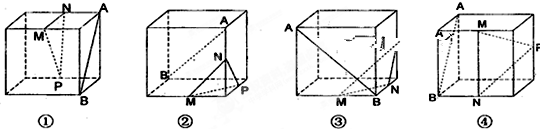
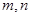 是两条不同的直线,
是两条不同的直线,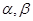 是两个不同的平面,则下列正确命题的序号是 .
是两个不同的平面,则下列正确命题的序号是 . ,
,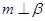 ,则
,则 ; ②.若
; ②.若 ,则
,则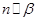 ;
;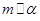 ,
,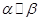 ; ④.若
; ④.若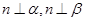 ,则
,则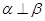 .
. A1B1C1D1中,E、F分别为BB1、CC1的中点,那么异面直线AE与D1F所成角的余弦值为 .
A1B1C1D1中,E、F分别为BB1、CC1的中点,那么异面直线AE与D1F所成角的余弦值为 .