题目内容
若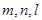 是互不重合的直线,
是互不重合的直线,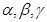 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题:
①若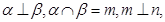 则
则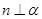 或
或 ;
;
②若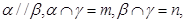 则
则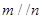 ;
;
③若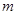 不垂直于
不垂直于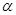 ,则
,则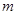 不可能垂直于
不可能垂直于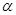 内的无数条直线;
内的无数条直线;
④若 且
且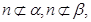 则
则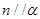
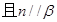 ;
;
⑤若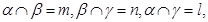 且
且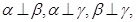 则
则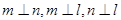 .
.
其中正确命题的序号是 .
②④⑤
解析试题分析:①由面面垂直性质定理知:当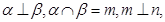 且
且 时,才有
时,才有 ;所以①错;
;所以①错;
②因为两平行平面被第三平面截得的交线平行,所以②对;
③命题“若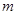 不垂直于
不垂直于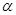 ,则
,则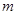 不可能垂直于
不可能垂直于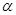 内的无数条直线”的逆否命题为“若
内的无数条直线”的逆否命题为“若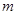 垂直于
垂直于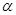 内的无数条直线,则
内的无数条直线,则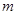 垂直于
垂直于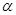 ”,这不符线面垂直判定定理,所以③错;
”,这不符线面垂直判定定理,所以③错;
④因为 所以
所以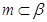 又
又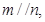
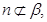 所以由线面平行判定定理得
所以由线面平行判定定理得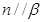 ,同理可得
,同理可得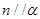 ,所以④对;
,所以④对;
⑤利用一个结论,两相交平面同垂直于第三平面,则它们交线垂直于第三平面,所以⑤对.
考点:线面平行与垂直判定定理,面面垂直性质定理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
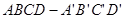 的外接球直径为
的外接球直径为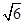 ,底面边长
,底面边长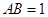 ,则侧棱
,则侧棱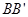 与平面
与平面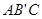 所成角的正切值为_________。
所成角的正切值为_________。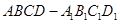 中,点
中,点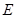 是棱
是棱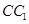 上的一个动点,平面
上的一个动点,平面 交棱
交棱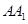 于点
于点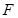 .给出下列四个结论:
.给出下列四个结论: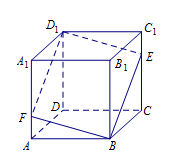
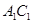 //平面
//平面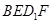 ;
;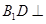 平面
平面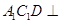 平面
平面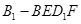 的体积均不变.
的体积均不变.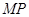 与
与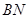 垂直的点
垂直的点 所构成的轨迹的周长等于 .
所构成的轨迹的周长等于 . A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 .
A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|=3|NC1|,则MN的长为 . 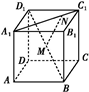
 .
.