题目内容
18.解不等式:(1)5x+2>2;
(2)33-x<6.
分析 (1)把不等式两边取以5为底数的对数,化为一次不等式求解;
(2)把不等式两边取以3为底数的对数,化为一次不等式求解.
解答 解:(1)由5x+2>2,得x+2>log52,即x>log52-2.
∴不等式5x+2>2的解集为(log52-2,+∞);
(2)由33-x<6,得3-x<log36=1+log32,即x>2-log32.
∴不等式33-x<6的解集为(2-log32,+∞).
点评 本题考查指数不等式的解法,考查了指数式和对数式的互化,是基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.数列{1+2n-1}的前n项的和为( )
| A. | 1+2n | B. | 2+2n | C. | n+2n-1 | D. | n+2+2n |
6.利用计算机在区间(0,1)上产生两个随机数a和b,则关于x的方程x2+2ax+b=0有实根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
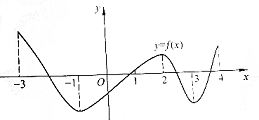 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.