题目内容
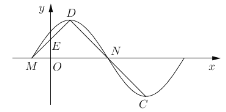
【题目】下图为函数![]() 的部分图象,
的部分图象,![]() 、
、![]() 是它与
是它与![]() 轴的两个交点,
轴的两个交点,![]() 、
、![]() 分别为它的最高点和最低点,
分别为它的最高点和最低点,![]() 是线段
是线段![]() 的中点,且
的中点,且![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 图象上的每个点的横坐标缩短为原来的一半,再向左平移
图象上的每个点的横坐标缩短为原来的一半,再向左平移![]() 个单位长度得到
个单位长度得到![]() 的图象,求
的图象,求![]() 的解析式及单调增区间,对称中心.
的解析式及单调增区间,对称中心.
【答案】(1)![]() ;
;
(2)![]() ;增区间:
;增区间:![]() (
(![]() );对称中心:
);对称中心:![]() (
(![]() );
);
【解析】
(1)由点![]() 的坐标可得出
的坐标可得出![]() 的值,再根据
的值,再根据![]() 为等腰直角三角形,可得出点
为等腰直角三角形,可得出点![]() 、
、![]() 的坐标,从而求出
的坐标,从而求出![]() 、
、![]() 的值,由此可得出函数
的值,由此可得出函数![]() 的解析式;
的解析式;
(2)根据三角函数变换规律求出函数![]() ,然后利用余弦函数的单调性和对称性可求出函数
,然后利用余弦函数的单调性和对称性可求出函数![]() 的单调增区间和对称中心的坐标.
的单调增区间和对称中心的坐标.
(1)由已知点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() ,
,
又![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,![]() ,则点
,则点![]() ,则
,则![]() ,
,
![]() ,解得
,解得![]() ,
,![]() .
.
将点![]() 的坐标代入函数
的坐标代入函数![]() 的解析式得
的解析式得![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,解得
,解得![]() ,
,
因此,![]() ;
;
(2)将函数![]() 图象上的每个点的横坐标缩短为原来的一半,得出函数
图象上的每个点的横坐标缩短为原来的一半,得出函数![]() 的图象,再向左平移
的图象,再向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() ,
,
由![]() ,得
,得![]() .
.
令![]() ,解得
,解得![]() .
.
因此,函数![]() 的单调增区间为
的单调增区间为![]() ,对称中心为
,对称中心为![]() .
.

练习册系列答案
相关题目