题目内容
已知关于x的方程|x|=ax+1有一个负根而且没有正根,则实数a的取值范围是( )
分析:法一:由已知方程|x|=ax+1有一个负根而且没有正根,可得出x<0,去掉绝对值符号即可解题.
法二:构造函数y=|x|,y=ax+1,在坐标系内作出函数图象,通过数形结合求出a的范围.
法二:构造函数y=|x|,y=ax+1,在坐标系内作出函数图象,通过数形结合求出a的范围.
解答:解:法一:如果x<0,|x|=-x,
-x=ax+1,x=-
<0,a+1>0,
a>-1;
如果x>0,|x|=x,x=ax+1,x=
>0,1-a>0,
a<1.
 因为没有正根,
因为没有正根,
所以a<1不成立.
所以a≥1.
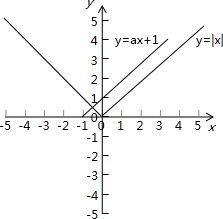
法二:令y=|x|,y=ax+1,在坐标系内作出函数图象,
方程|x|=ax+1有一个负根,
但没有正根,由图象可知
a≥1
故选A.
-x=ax+1,x=-
| 1 |
| 1+a |
a>-1;
如果x>0,|x|=x,x=ax+1,x=
| 1 |
| 1-a |
a<1.
 因为没有正根,
因为没有正根,所以a<1不成立.
所以a≥1.
法二:令y=|x|,y=ax+1,在坐标系内作出函数图象,
方程|x|=ax+1有一个负根,
但没有正根,由图象可知
a≥1
故选A.
点评:本题考查了含绝对值符号的一元一次方程、根的存在性及根的个数判断,难度适中,法一关键是根据已知条件列出关于a的不等式.法二关键是数形结合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目