题目内容
已知关于x的方程| |x| | x+3 |
分析:此题必有一根为0,利用变量分离得到
=
,再利用数形结合的思想得出方程有两个不等的实根时K的范围.
| 1 |
| k |
|
解答: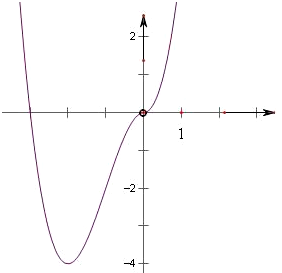 解:由题意得:
解:由题意得:
=
,
利用导函数得到原函数的单调性,找到极值点,
当x∈(0,+∞),y'=3x2+6x=0,解得x=0或-2
当x∈(0,+∞)时,y'>0
当x∈(-∞,0),y'=-3x2-6x=0,解得x=0或-2
当x∈(-∞,-2)时,y'<0,当x∈(-2,0)时,y'>0
∴x=-2处取极小值
画出等式右边函数的草图知-4<
<0或
>0;
即K得范围为k>0或k< -
 解:由题意得:
解:由题意得:| 1 |
| k |
|
利用导函数得到原函数的单调性,找到极值点,
当x∈(0,+∞),y'=3x2+6x=0,解得x=0或-2
当x∈(0,+∞)时,y'>0
当x∈(-∞,0),y'=-3x2-6x=0,解得x=0或-2
当x∈(-∞,-2)时,y'<0,当x∈(-2,0)时,y'>0
∴x=-2处取极小值
画出等式右边函数的草图知-4<
| 1 |
| k |
| 1 |
| k |
即K得范围为k>0或k< -
| 1 |
| 4 |
点评:本题主要考查了函数与方程的综合运用,以及此题关键在于利用导函数画出函数草图,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目