题目内容
【题目】解答
(1)在区间[1,3]上任取两整数a、b,求二次方程x2+2ax+b2=0有实数根的概率.
(2)在区间[1,3]上任取两实数a、b,求二次方程x2+2ax+b2=0有实数根的概率.
【答案】
(1)解:在区间[1,3]上任取两整数a、b,共有3×3=9种取法,基本事件共9个,(1,1),(1,2),(1,3),
(2,1),(2,2),(2,3),(3,1),(3,2),(3,3).其中第一个数表示a的取值,第二个数表示b的取值.
使二次方程x2+2ax+b2=0有实数根的事件为A,A中A,B满足a≥b,则事件A中包含6基本事件.
事件A发生的概率为P(A)= ![]()
(2)解:试验的全部结果所构成的区域为{(a,b)|1≤a≤3,1≤b≤3}.
构成事件A的区域为{(a,b)|1≤a≤3,1≤b≤3,a≥b}.
如图,
∴所求的概率P(A)= ![]() .
.
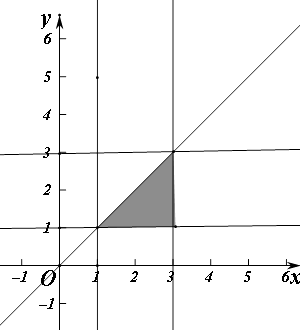
【解析】(1)由一元二次方程的判别式大于等于0得到方程x2+2ax+b2=0有实数根的充要条件为a≥b,用列举法求出a,b是从[0,3]任取的两个整数即从0,1,2,3四个数中任取的两个数,查出满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;(2)由题意求出点(a,b)所构成的正方形的面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率
【考点精析】认真审题,首先需要了解几何概型(几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等).

 名校课堂系列答案
名校课堂系列答案【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对照数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)求y关于x的线性回归方程;(已知 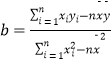 )
)
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤.