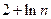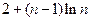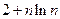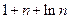题目内容
已知数列{an},且x=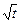 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
(1)求数列{an}的通项公式;
(2)记bn=2(1-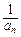 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
(3)若cn=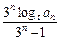 ,证明:
,证明: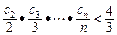 ( n∈N﹡).
( n∈N﹡).
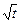 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .(1)求数列{an}的通项公式;
(2)记bn=2(1-
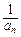 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;(3)若cn=
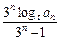 ,证明:
,证明: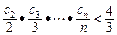 ( n∈N﹡).
( n∈N﹡).解:(1)f ′(x)=3an-1x2-3[(t+1)an-an+1],
所以f ′(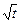 )=3an-1t-3[(t+1)an-an+1]=0.
)=3an-1t-3[(t+1)an-an+1]=0.
整理得:an+1-an=t(an-an-1) .…………………………………………2分
当 t=1时,{an-an-1}是常数列,得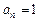 ;
;
当 t≠1时{an-an-1}是以 a2-a1=t2-t为首项, t为公比的等比数列,
所以 an-an-1=(t2-t)·t n-2=(t-1)·t n-1.
方法一:由上式得
(an-an-1)+(an-1-an-2)+…+(a2-a1)=(t-1)(tn-1+tn-2+…+t),
即 an-a1=(t-1)·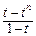 =tn-t,
=tn-t,
所以 an=tn(n≥2) .
又,当t=1时上式仍然成立,故 an=tn(n∈N﹡) .………………………4分
方法二:由上式得: an-tn=an-1-tn-1,
所以{an-tn}是常数列,an-tn=a1-t=0 an=tn(n≥2) .
又,当t=1时上式仍然成立,故 an=tn(n∈N﹡) .
(2)当t=2, bn=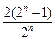 =2-
=2-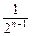 .
.
∴Sn=2n-(1+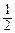 +
+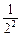 +…+
+…+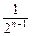 )=2n-
)=2n-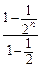
=2n-2(1-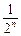 )=2n-2+2·
)=2n-2+2·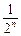
由Sn>2010,得
2n-2+2(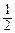 )n>2010, n+(
)n>2010, n+(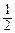 )n>1006,
)n>1006,
当n≤1005时, n+(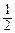 )n<1006,
)n<1006,
当 n≥1006时, n+(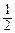 )n>1006,
)n>1006,
因此 n的最小值为1006.………………………………………………8分
(3)cn=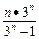 且c1=
且c1=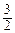 ,所以
,所以
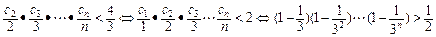 .
.
因为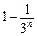 =
=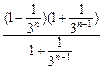 =
=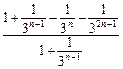
=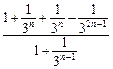 ≥
≥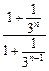 ,
,
所以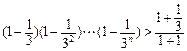
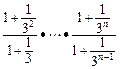 =
=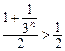 .
.
从而原命题得证.…………………………………………………………14分
所以f ′(
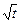 )=3an-1t-3[(t+1)an-an+1]=0.
)=3an-1t-3[(t+1)an-an+1]=0.整理得:an+1-an=t(an-an-1) .…………………………………………2分
当 t=1时,{an-an-1}是常数列,得
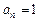 ;
;当 t≠1时{an-an-1}是以 a2-a1=t2-t为首项, t为公比的等比数列,
所以 an-an-1=(t2-t)·t n-2=(t-1)·t n-1.
方法一:由上式得
(an-an-1)+(an-1-an-2)+…+(a2-a1)=(t-1)(tn-1+tn-2+…+t),
即 an-a1=(t-1)·
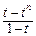 =tn-t,
=tn-t,所以 an=tn(n≥2) .
又,当t=1时上式仍然成立,故 an=tn(n∈N﹡) .………………………4分
方法二:由上式得: an-tn=an-1-tn-1,
所以{an-tn}是常数列,an-tn=a1-t=0 an=tn(n≥2) .
又,当t=1时上式仍然成立,故 an=tn(n∈N﹡) .
(2)当t=2, bn=
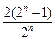 =2-
=2-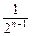 .
.∴Sn=2n-(1+
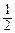 +
+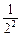 +…+
+…+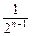 )=2n-
)=2n-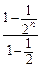
=2n-2(1-
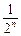 )=2n-2+2·
)=2n-2+2·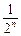
由Sn>2010,得
2n-2+2(
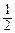 )n>2010, n+(
)n>2010, n+(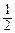 )n>1006,
)n>1006, 当n≤1005时, n+(
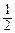 )n<1006,
)n<1006,当 n≥1006时, n+(
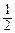 )n>1006,
)n>1006,因此 n的最小值为1006.………………………………………………8分
(3)cn=
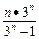 且c1=
且c1=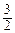 ,所以
,所以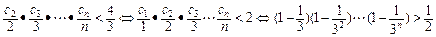 .
.因为
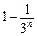 =
=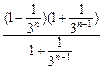 =
=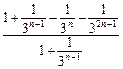
=
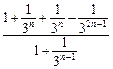 ≥
≥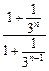 ,
,所以
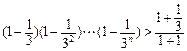
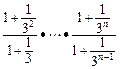 =
=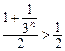 .
.从而原命题得证.…………………………………………………………14分
略

练习册系列答案
相关题目
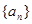 的前n项的和
的前n项的和 ,那么这个数列的通项公式为( )
,那么这个数列的通项公式为( )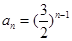
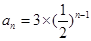
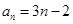
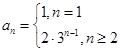
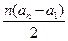 .
.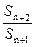 +
+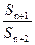 ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;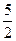 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。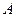 :
: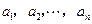 ,若满足
,若满足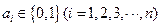 ,则称数列
,则称数列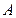 为“0-1
为“0-1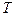 ,
, :
: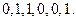 设
设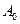 是“0-1数列”,令
是“0-1数列”,令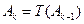 ,
,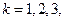 …。
…。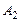 :
: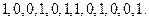 求数列
求数列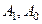 ;
;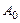 共有10项,则数列
共有10项,则数列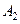 中连续两项
中连续两项 相等的数对至少有多少对?请说明理由;
相等的数对至少有多少对?请说明理由;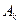 中连续两项都是0的数对
中连续两项都是0的数对 个数为
个数为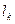 ,
,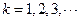 ,
,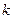 的表达式
的表达式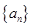 为等差数列,且
为等差数列,且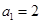 ,
,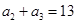 ,那么则
,那么则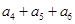 等于
等于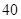
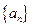 中,若
中,若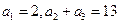 ,则
,则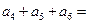
 满分13分)
满分13分)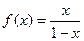 ,若数列
,若数列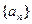 满足
满足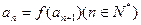 ,且
,且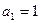 .
.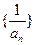 是等差数列;
是等差数列;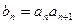 (
(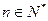 ),设数列
),设数列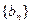 的前
的前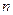 项和为
项和为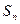 ,求使得
,求使得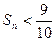 成立的
成立的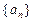 中,已知
中,已知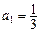 ,
,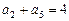 ,
,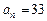 ,则n为
,则n为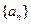 中,
中,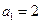 ,
, 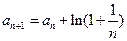 ,则
,则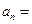 ( )
( )