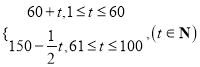题目内容
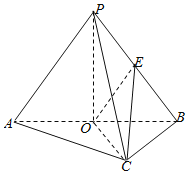
【题目】已知三棱锥P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中点,E是PB中点.
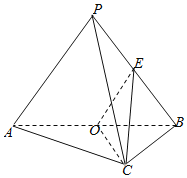
(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
【答案】(1)见解析(2)![]()
【解析】
(1)连结PO,利用等腰三角形的性质证得![]() ,利用勾股定理计算证明证得
,利用勾股定理计算证明证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)利用等体积法,由![]() 列方程,解方程求得
列方程,解方程求得![]() 到平面
到平面![]() 的距离.
的距离.
(1)连结PO,在△PAB中,PA=PB,O是AB中点,
∴PO⊥AB,
又∵AC=BC=2,AC⊥BC,∴![]() .
.
∵PA=PB=3,∴![]() ,PC2=PO2+OC2,
,PC2=PO2+OC2,
∴PO⊥OC.
又AB∩OC=O,AB平面ABC,OC平面ABC,
∴PO⊥平面ABC,
∵PO平面PAB,∴平面PAB⊥平面ABC.
(2)∵OE是△PAB的中位线,∴![]() .
.
∵O是AB中点,AC=BC,∴OC⊥AB.
又平面PAB⊥平面ABC,两平面的交线为AB,∴OC⊥平面PAB,
∵OE平面PAB,∴OC⊥OE.
设点B到平面OEC的距离为d,则VB﹣OEC=VE﹣OBC,
∴![]() ,
,
∴点B到平面OEC的距离:
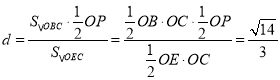 .
.

【题目】已知抛物线C:y2=2x的焦点为F,过焦点F的直线交抛物线于A,B两点,过A,B作准线的垂线交准线与P,Q两点.R是PQ的中点.
(1)证明:以PQ为直径的圆恒过定点F.
(2)证明:AR∥FQ.
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.