题目内容
2.有标号为1,2,3,4,5,6的六个小球,从中选出四个放入标号为1,2,3,4的四个盒中,每盒只放一个小球.
(1)求奇数号盒只放奇数号小球的不同放法数;
(2)求奇数号小球必须放在奇数号盒中的不同放法数.
(3)若不许空盒且将六个小球都放入盒中,求所有不同的放法数.
分析 (1)根据题意,分2步进行分析:①、奇数号盒只放奇数号小球,每盒只放一个小球,②、将剩余的4个小球中的2个放入余下的两个盒中,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(2)根据题意,分两类讨论:①取出1个奇数号小球和3个偶数号小球共4球放入,②取出2个奇数号小球和2个偶数号小球共4球放入,分别求出每一类的情况数目,由分类计数原理计算可得答案;
(3)由于盒不空且6个小球都要放入,所以考虑先对6个小球进行先分组再放入盒中,分2种情况讨论:①将6个小球分成1,1,1,3四组,再放入四个盒中,②将6个小球分成1,1,2,2四组,再放入四个盒中,分别求出每一类的情况数目,由分类计数原理计算可得答案.
解答 解:(1)∵奇数号盒只放奇数号小球,每盒只放一个小球
∴先从3个奇数号小球中任取2个放入奇数号盒,有6种放法
再将剩余的4个小球中的2个放入余下的两个盒中,有12种放法
∴不同放法数为N1=6×12=72种;…(4分)
(2)∵奇数号小球必须放在奇数号盒中,每盒只放一个小球,
∴需分两类讨论:
①取出1个奇数号小球和3个偶数号小球共4球放入,共有C31C21A33=36种;
②取出2个奇数号小球和2个偶数号小球共4球放入,A32A32=36种
∴所有不同放法数为N2=36+36=72种;…(8分)
(3)由于盒不空且6个小球都要放入,所以考虑先对6个小球进行先分组再放入盒中,
分2种情况讨论:
①将6个小球分成1,1,1,3四组的不同分组方法数为C63,再放入四个盒中有A44种,
②将6个小球分成1,1,2,2四组的不同分组方法数为$\frac{1}{2}$C62C42,再放入四个盒中有A44种,
∴所有不同放法数为N3=C63×A44+$\frac{1}{2}$C62C42×A44=1560种.…(12分)
点评 本题考查排列组合的综合运用,涉及分步、分类计数原理的应用,关键要认真分析题意,确定满足题意的分类或分步分析的步骤.

 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | $\frac{{\sqrt{10}}}{4}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{5}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | a,b,c都是偶数 | B. | a,b,c至多有一个是偶数 | ||
| C. | a,b,c至少有一个是奇数 | D. | a,b,c都是奇数 |
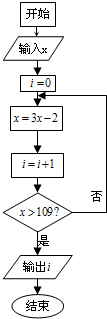
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
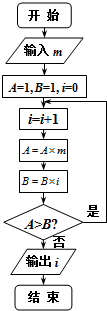
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |