题目内容
已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,离心率为
,离心率为![]() .直线
.直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点.设
的对称点.设![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() ,
,![]() 的周长为
的周长为![]() ,写出椭圆
,写出椭圆![]() 的方程;
的方程;
(Ⅲ)确定![]() 的值,使得
的值,使得![]() 是等腰三角形.
是等腰三角形.
(Ⅰ)证明过程见答案(Ⅱ)椭圆方程为![]() .(Ⅲ)
.(Ⅲ)![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
解析:
(Ⅰ)因为![]() 分别是直线
分别是直线![]() 与
与![]() 轴,
轴,![]() 轴的交点,所以
轴的交点,所以![]() 的坐标分别是
的坐标分别是![]() ,
,![]() .由
.由 得
得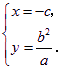 这里
这里![]() .
.
所以点![]() 的坐标是
的坐标是![]() .由
.由![]() 得
得![]() .
.
即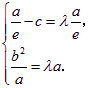 解得
解得![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,所以
,所以![]() .由
.由![]() 的周长为
的周长为![]() ,
,
得![]() .所以
.所以![]() .椭圆方程为
.椭圆方程为![]() .
.
(Ⅲ)因为![]() ,所以
,所以![]() 为钝角,要使
为钝角,要使![]() 为等腰三角形,必有
为等腰三角形,必有![]() ,即
,即![]() .
.
设点![]() 到
到![]() 的距离为
的距离为![]() ,由
,由![]() ,
,
得![]() .所以
.所以![]() .于是
.于是![]() .
.
即当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线