题目内容
(本小题满分12分)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
.
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线 的方程.
的方程.
【答案】
.解:
(Ⅰ)有条件有 ,解得
,解得 ,
, .
.
∴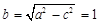
所以,所求椭圆的方程为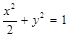 …………………………… 4分
…………………………… 4分
(Ⅱ)由(Ⅰ)知 、
、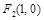 .
.
若直线l的斜率不存在,则直线l的方程为 .
.
将 代入椭圆方程得:
代入椭圆方程得: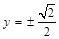 .
.
不妨设 、
、 ,
,
∴
∴ ,与题设矛盾.
,与题设矛盾.
所以,直线l的斜率存在.设直线l的斜率为k,则直线的方程为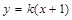 .
.
设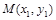 、
、 ,联立方程组
,联立方程组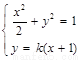 ,消y得:
,消y得:
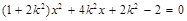
由根与系数的关系知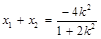 ,从而
,从而 .
.
又∵ ,
,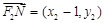
∴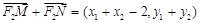
∴
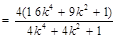
∴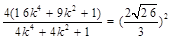 .
.
化简得:
解得: 或
或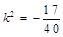
∴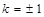
【解析】略

练习册系列答案
相关题目