题目内容
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).
【答案】
(Ⅰ)由已知可得 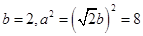 ,
,
所求椭圆方程为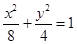 .
……4分
.
……4分
(Ⅱ)若直线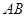 的斜率存在,设
的斜率存在,设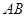 方程为
方程为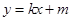 ,依题意
,依题意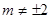 .
.
设 ,
,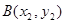 ,
,
由  得
得 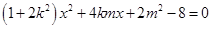 . ……6分
. ……6分
则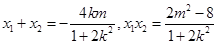 . 由已知
. 由已知 ,
,
所以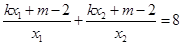 ,即
,即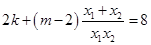 . ……8分
. ……8分
所以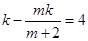 ,整理得
,整理得 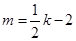 .
.
故直线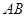 的方程为
的方程为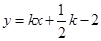 ,即
,即 (
(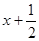 )
)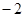 .
.
所以直线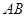 过定点(
过定点(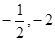 ). ………10分
). ………10分
若直线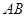 的斜率不存在,设
的斜率不存在,设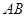 方程为
方程为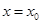 ,
,
设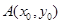 ,
,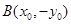 ,由已知
,由已知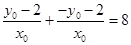 ,
,
得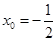 .此时
.此时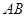 方程为
方程为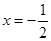 ,显然过点(
,显然过点(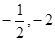 ).
).
综上,直线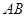 过定点(
过定点(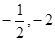 ).
).
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线