Question

【题目】有人玩掷均匀硬币走跳棋的游戏，棋盘上标有第0站（出发地），在第1站，第2站，……，第100站. 一枚棋子开始在出发地，棋手每掷一次硬币，这枚棋子向前跳动一次，若掷出正向，棋子向前跳一站，若掷出反面，棋子向前跳两站，直到棋子跳到第99站（失败收容地）或跳到第100站（胜利大本营），该游戏结束. 设棋子跳到第站的概率为.

（1）求，，；

（2）写出与、的递推关系）；

（3）求玩该游戏获胜的概率.

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）结合题设条件能够求出，，；

（2）依题意，棋子跳到第站有两种可能：第一种，棋子先到站，又掷出反面，其概率为；第二种，棋子先到站，又掷出正面，其概率为，由此能够得到与的递推关系；

（3）由，知数列是以为首项，为公比的等比数列，由此利用等比数列求和公式得到结果.

（1）依题意得，，

（2）依题意知，棋子跳到第站有两种情况：

第一种，棋子先到站，又掷出反面，其概率为；

第二种，棋子先到站，又掷出正面，其概率为.

∴

（3）由（2）知，，且

∴是以为首项，为公比的等比数列.

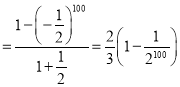
又 ∴或

∴玩该游戏获胜的概率为.