题目内容
已知 是不全为
是不全为 的实数,函数
的实数,函数 ,
, ,方程
,方程 有实根,且
有实根,且 的实数根都是
的实数根都是 的根,反之,
的根,反之, 的实数根都是
的实数根都是 的根.
的根.
(1)求 的值;(2)若
的值;(2)若 ,求
,求 的取值范围.
的取值范围.
(1)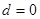 ,(2)
,(2)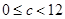 .
.
解析试题分析:(1)本小题中对已知条件的理解是一个关键点,可设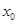 是
是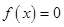 的根,因此有
的根,因此有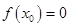 ,又
,又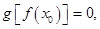 则有
则有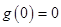 ,从而对于函数
,从而对于函数 而言,可得
而言,可得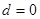 .
.
(2)本小题中因为有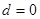 ,所以
,所以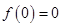 ,又可知
,又可知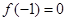 ,所以
,所以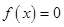 的根为0和-1,对于实数
的根为0和-1,对于实数 以下分为正数,负数与零三种情况进行讨论.
以下分为正数,负数与零三种情况进行讨论.
试题解析:(1)设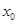 是
是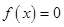 的根,那么
的根,那么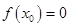 ,则
,则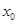 是
是 的根,则
的根,则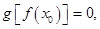 即
即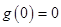 ,所以
,所以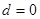 .
.
(2) ,所以
,所以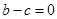 ,即
,即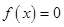 的根为0和-1,
的根为0和-1,
①当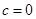 时,则
时,则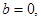 这时
这时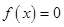 的根为一切实数,而
的根为一切实数,而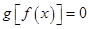 ,所以
,所以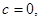 符合要求.
符合要求.
当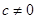 时,因为
时,因为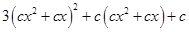 =0的根不可能为0和
=0的根不可能为0和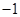 ,所以
,所以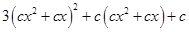 必无实数根,
必无实数根,
②当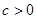 时,
时,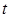 =
=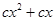 =
=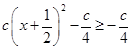 ,即函数
,即函数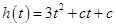 在
在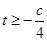 ,
,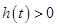 恒成立,又
恒成立,又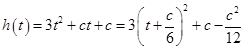 ,所以
,所以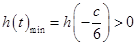 ,即
,即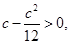 所以
所以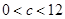 ;③当
;③当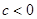 时,
时,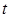 =
=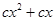 =
=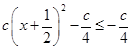 ,即函数
,即函数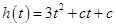 在
在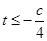 ,
,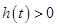 恒成立,又
恒成立,又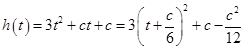 ,所以
,所以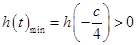 ,
,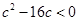 ,而
,而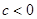 ,舍去,综上所述,所以
,舍去,综上所述,所以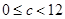 .
.
考点:函数的零点概念(方程的根),复合函数概念,函数值域问题,配方法,分类讨论思想.

练习册系列答案
相关题目
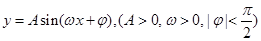 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是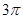 ,又:图象过点
,又:图象过点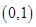 ,
, 的集合;
的集合; ,当
,当 时,恒有
时,恒有 .
. 为正实数,
为正实数, ,并且
,并且 ,试求
,试求 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有

 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围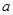 为实数,
为实数,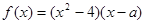 .
.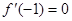 ,求
,求 在
在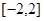 上的最大值和最小值;
上的最大值和最小值;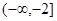 和
和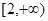 上都是递增的,求
上都是递增的,求
 的奇偶性;
的奇偶性; 时,
时, 恒成立,求b的取值范围.
恒成立,求b的取值范围.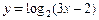 的定义域是 .
的定义域是 . 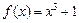 的反函数
的反函数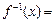 .
.