题目内容
已知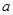 为实数,
为实数,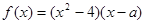 .
.
(1)若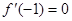 ,求
,求 在
在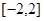 上的最大值和最小值;
上的最大值和最小值;
(2)若 在
在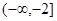 和
和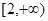 上都是递增的,求
上都是递增的,求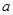 的取值范围.
的取值范围.
(1) ,
,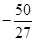 ;(2)
;(2)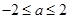 .
.
解析试题分析:解题思路:(1)求导函数,利用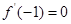 ,解得
,解得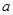 的值;再求最值;(2)利用“若函数
的值;再求最值;(2)利用“若函数 在某区间上单调递增,则
在某区间上单调递增,则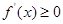 在该区间恒成立”求解.规律总结:(1)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值;(2)若函数
在该区间恒成立”求解.规律总结:(1)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值;(2)若函数 在某区间上单调递增,则
在某区间上单调递增,则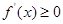 在该区间恒成立;“若函数
在该区间恒成立;“若函数 在某区间上单调递减,则
在某区间上单调递减,则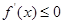 在该区间恒成立.
在该区间恒成立.
试题解析:(1)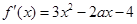 .
.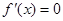 时,
时,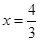 或
或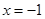 ,
, 在
在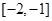 上单调递增,在
上单调递增,在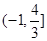 上上单调递减,在
上上单调递减,在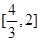 上单调递增;所以
上单调递增;所以 在
在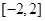 上的最大值为
上的最大值为 ,最小值为
,最小值为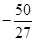 .
.
(2)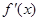 的图象为过
的图象为过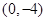 ,开口向上的抛物线由题
,开口向上的抛物线由题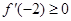 且
且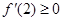 解得
解得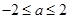 .
.
考点:1.求函数的最值;2.根据函数的单调性求参数.

练习册系列答案
相关题目
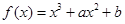 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线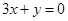 平行.
平行. 的解析式;
的解析式;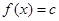 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围 是不全为
是不全为 的实数,函数
的实数,函数 ,
, ,方程
,方程 有实根,且
有实根,且 的根,反之,
的根,反之, 的值;(2)若
的值;(2)若 ,求
,求 的取值范围.
的取值范围.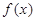 是定义在
是定义在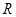 上的奇函数,当
上的奇函数,当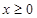 时,
时, .
. ;
;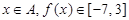 ,求区间
,求区间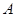 .
. 为常数,
为常数, ,函数
,函数 ,
, 且方程
且方程 有等根.
有等根. 的解析式及值域;
的解析式及值域; ,
, ,若
,若 ,求实数
,求实数 的取值范围;
的取值范围;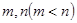 ,使
,使 的定义域和值域分别为
的定义域和值域分别为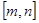 和
和 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.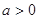 且
且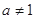 ,函数
,函数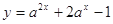 在
在 的最大值是14,求
的最大值是14,求 的值。
的值。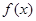 是定义在区间
是定义在区间 上的奇函数,且
上的奇函数,且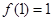 ,若
,若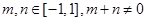 时,有
时,有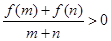 .
.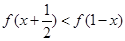 ;
;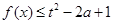 对
对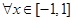 与
与 恒成立,求实数
恒成立,求实数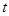 的取值范围.
的取值范围.
 .
. 的奇偶性;
的奇偶性; 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.
 ,则方程
,则方程 的解集为 .
的解集为 .