题目内容
已知函数 ,当
,当 时,恒有
时,恒有 .
.
(1)求证: 是奇函数;
是奇函数;
(2)如果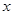 为正实数,
为正实数, ,并且
,并且 ,试求
,试求 在区间[-2,6]上的最值.
在区间[-2,6]上的最值.
(1)证明见解析;(2)最大值为1,最小值为-3..
解析试题分析:解题思路:(1)利用奇函数的定义进行证明;(2)先证明 的单调性,再求在
的单调性,再求在 的最值.
的最值.
规律总结:(1)证明函数奇偶性的步骤:①验证函数定义域是否关于原点对称,②判断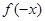 与
与 的关系,③下结论;(2)先利用函数单调性的定义证明函数的单调性,再根据单调性求最值.注意点:判定或证明函数的奇偶性时,一定不要忘记验证函数的定义域是否关于原点对称.
的关系,③下结论;(2)先利用函数单调性的定义证明函数的单调性,再根据单调性求最值.注意点:判定或证明函数的奇偶性时,一定不要忘记验证函数的定义域是否关于原点对称.
试题解析: (1)函数定义域为 ,其定义域关于原点对称,
,其定义域关于原点对称,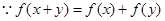 ,令
,令 ,
, ,令
,令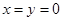 ,
, ,得
,得 .
.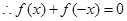 ,得
,得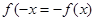 ,
, 为奇函数.
为奇函数.
(2)设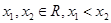 .
.
则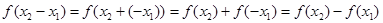 .
. ,
, ,
, ,即
,即 在
在 上单调递减.
上单调递减. 为最大值,
为最大值, 为最小值.
为最小值.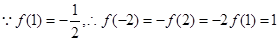 ,
,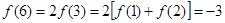 .
.
∴ 在区间
在区间 上的最大值为1,最小值为-3.
上的最大值为1,最小值为-3.
考点:1.函数的奇偶性;2.函数的最值.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 的图象上一点P(1,0),且在P点处的切线与直线
的图象上一点P(1,0),且在P点处的切线与直线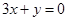 平行.
平行. 的解析式;
的解析式;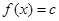 在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
在区间[1,3]上恰有两个相异的实根,求实数c的取值范围
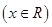 满足
满足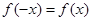 ,
,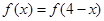 ,且当
,且当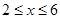 时,
时,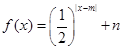 .
.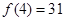 ,求
,求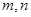 的值.
的值. 是不全为
是不全为 的实数,函数
的实数,函数 ,
,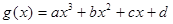 ,方程
,方程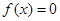 有实根,且
有实根,且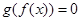 的根,反之,
的根,反之, 的值;(2)若
的值;(2)若 ,求
,求 的取值范围.
的取值范围.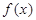 是定义在
是定义在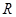 上的奇函数,当
上的奇函数,当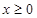 时,
时,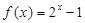 .
.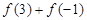 ;
;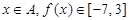 ,求区间
,求区间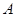 .
. 且
且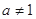 ,函数
,函数 在
在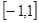 的最大值是14,求
的最大值是14,求 的值。
的值。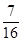 ,分别求f1(x)和f2(x);
,分别求f1(x)和f2(x);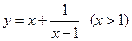 的最小值为 .
的最小值为 . 的反函数为
的反函数为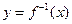 ,则方程
,则方程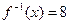 的解
的解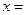 .
.