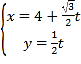题目内容
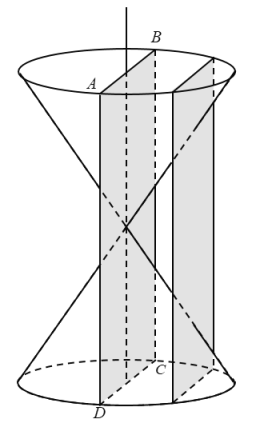
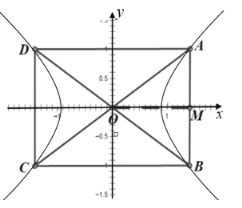
【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图，将两个完全相同的圆锥对顶放置（两圆锥的轴重合），已知两个圆锥的底面半径为1，母线长均为
，记过圆锥轴的平面ABCD为平面
（与两个圆锥面的交线为AC、BD），用平行于的平面截圆锥，该平面与两个圆锥侧面的截线即为双曲线E的一部分，且双曲线E的两条渐近线分别平行于AC、BD，则双曲线E的离心率为（ ）
A.
B.C.
D.2
【答案】B
【解析】
以矩形
的中心为原点，圆锥的轴为x轴建立平面直角坐标系，由题，得
，从而可得到本题答案.
以矩形的中心为原点，圆锥的轴为x轴建立平面直角坐标系，
设双曲线的标准方程为
，
由题，得
，则
，即，
所以
.
故选：B
练习册系列答案
相关题目
