题目内容
【题目】设集合![]() 表示具有下列性质的函数
表示具有下列性质的函数![]() 的集合:①
的集合:①![]() 的定义域为
的定义域为![]() ;②对任意
;②对任意![]() ,都有
,都有![]()
(1)若函数![]() ,证明
,证明![]() 是奇函数;并当
是奇函数;并当![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)设函数![]() (a为常数)是奇函数,判断
(a为常数)是奇函数,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(3)在(2)的条件下,若 ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析,![]() ,
,![]()
(2)![]() ,证明见解析
,证明见解析
(3)![]() 或
或![]() 时,3个零点;
时,3个零点;![]() 或
或![]() 时,1个零点;
时,1个零点;![]() 时,5个零点.
时,5个零点.
【解析】
(1)利用赋值法和奇函数的定义证明函数是奇函数,由题得![]() 的方程组,解方程组即得解;(2)先求出a的值,再利用
的方程组,解方程组即得解;(2)先求出a的值,再利用![]() 的定义证明;(3)令h(x)=t,则h(t)=2,再分类讨论数形结合分析得解.
的定义证明;(3)令h(x)=t,则h(t)=2,再分类讨论数形结合分析得解.
(1)令![]() 得
得![]() .
.
令![]() ,
,![]() ,所以函数
,所以函数![]() 是奇函数.
是奇函数.
![]() ,
,![]()
解上面关于![]() 的方程组得
的方程组得![]() ,
,![]() .
.
(2)因为函数![]() (a为常数)是奇函数,
(a为常数)是奇函数,
所以![]() .满足函数g(x)是奇函数.
.满足函数g(x)是奇函数.
设![]() ,所以
,所以![]() ,
,
因为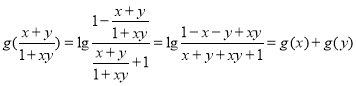 ,
,
所以![]() .
.
(3)令![]() .
.
令h(x)=t,则h(t)=2,
所以函数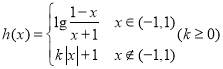
当k=0时,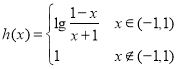 ,则
,则![]() ,此时只有一个解,一个零点;
,此时只有一个解,一个零点;
当![]() 时,只有一个
时,只有一个![]() ,对应三个零点;
,对应三个零点;
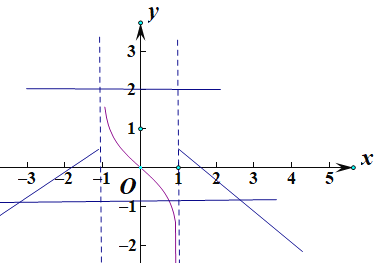
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
![]() ,
,
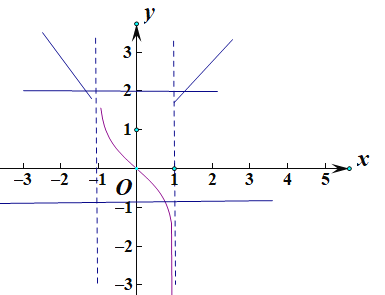
所以在![]() ,
,![]() ,三个t各对应一个零点,共三个零点;
,三个t各对应一个零点,共三个零点;
当![]() ,
,![]() ,三个t各对应一个,一个,三个零点,共五个零点;
,三个t各对应一个,一个,三个零点,共五个零点;
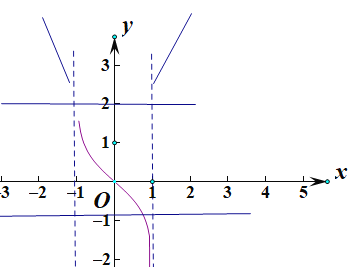
当![]() 时,h(t)=2只有一个解,
时,h(t)=2只有一个解,![]() ,对应一个零点.
,对应一个零点.
综合得![]() 或
或![]() 时,3个零点;
时,3个零点;![]() 或
或![]() 时,1个零点;
时,1个零点;![]() 时,5个零点.
时,5个零点.

练习册系列答案
相关题目