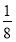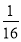题目内容
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数字-1,0,1,2.称“从盒中随机抽取一张,记下卡片上的数字后并放回”为一次试验(设每次试验的结果互不影响).
(1)在一次试验中,求卡片上的数字为正数的概率;
(2)在四次试验中,求至少有两次卡片上的数字都为正数的概率;
(3)在两次试验中,记卡片上的数字分别为X,η,试求随机变量X=X·η的分布列与数学期望E(X).
(1)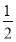 (2)
(2)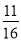 (3)
(3)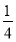
【解析】(1)记事件A为“在一次试验中,卡片上的数字为正数”,则P(A)=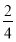 =
=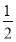 .
.
(2)记事件B为“在四次试验中,至少有两次卡片上的数字都为正数”.由(1)可知在一次试验中,卡片上的数字为正数的概率是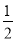 .所以P(B)=1-
.所以P(B)=1-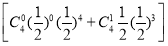 =
=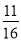 .
.
(3)由题意可知,X,η的可能取值都为-1,0,1,2,
所以随机变量X的可能取值为-2,-1,0,1,2,4.
P(X=-2)=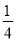 ×
× ×2=
×2=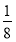 ;
;
P(X=-1)= ×
× ×2=
×2=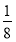 ;
;
P(X=0)=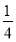 ×
×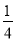 ×7=
×7=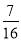 ;
;
P(X=1)= ×
×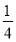 ×2=
×2=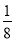 ;
;
P(X=2)=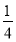 ×
× ×2=
×2=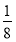 ;
;
P(X=4)= ×
× =
=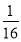 .
.
所以随机变量X的分布列为
X | -2 | -1 | 0 | 1 | 2 | 4 |
P |
|
|
|
|
|
|
所以E(X)=-2×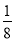 -1×
-1× +0×
+0×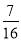 +1×
+1×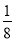 +2×
+2×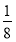 +4×
+4×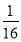 =
=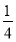 .
.

练习册系列答案
相关题目