题目内容
如图,在矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将△AOD折起,使DB= .
.

(1)求证:平面AOD⊥平面ABCO;
(2)求直线BC与平面ABD所成角的正弦值.
(1)见解析(2)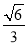
【解析】(1)证明:∵在矩形ABCD中,AB=2AD=2,O为CD中点,
∴△AOD,△BOC为等腰直角三角形,∴∠AOB=90°,即OB⊥OA.
取AO中点H,连接DH,BH,则OH=DH=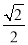 ,
,
在Rt△BOH中,BH2=BO2+OH2=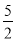 ,
,
在△BHD中,DH2+BH2=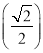 2+
2+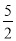 =3,又DB2=3,
=3,又DB2=3,
∴DH2+BH2=DB2,∴DH⊥BH.
又DH⊥OA,OA∩BH=H,∴DH⊥面ABCO,而DH?平面AOD,∴平面AOD⊥平面ABCO.
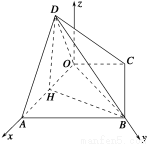
(2)解 分别以OA,OB所在直线为x轴和y轴,O为坐标原点,建立如图所示的空间直角坐标系,则B(0,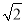 ,0),A(
,0),A(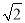 ,0,0),D
,0,0),D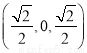 ,C
,C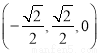 .
.
∴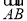 =(-
=(-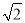 ,
,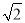 ,0),
,0), =
= ,
,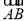 =
= .
.
设平面ABD的一个法向量为n=(x,y,z),
由 得
得
即x=y,x=z,令x=1,则y=z=1,取n=(1,1,1).
设α为直线BC与平面ABD所成的角,则sin α= =
=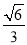 .
.
即直线BC与平面ABD所成角的正弦值为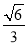 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目