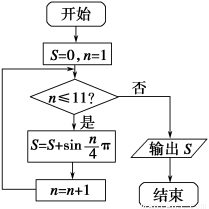
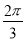题目内容
f(x)= 则下列关于y=f[f(x)]-2的零点个数判断正确( ).
则下列关于y=f[f(x)]-2的零点个数判断正确( ).
A.当k=0时,有无数个零点,
B.当k<0时,有3个零点
C.当k>0时,有3个零点
D.无论k取何值,都有4个零点
A
【解析】当k=0时,f(x)=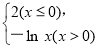 当x>1时,-ln x<0,所以f[f(x)]=f(-ln x)=2,所以此时y=f[f(x)]-2有无数个零点;当k<0时,y=f[f(x)]-2的零点即方程f[f(x)]=2的根,所以f(x)=0或f(x)=e-2,由图可知方程只有两根:
当x>1时,-ln x<0,所以f[f(x)]=f(-ln x)=2,所以此时y=f[f(x)]-2有无数个零点;当k<0时,y=f[f(x)]-2的零点即方程f[f(x)]=2的根,所以f(x)=0或f(x)=e-2,由图可知方程只有两根:
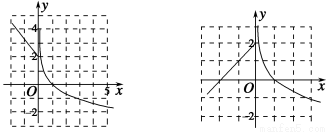
当k>0时,由图可知:f(x)=2有两根,所以由f[f(x)]=2得:f(x)=0或f(x)=e-2,又f(x)=0有两根,f(x)=e-2有两根,所以f[f(x)]=2有四根.

练习册系列答案
相关题目