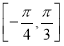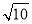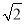Question

已知函数f(x)＝.

(1)函数f(x)在点(0，f(0))的切线与直线2x＋y－1＝0平行，求a的值；

(2)当x∈[0,2]时，f(x)≥恒成立，求a的取值范围．

 

Answer 1

（1）a＝3（2）

【解析】(1)f′(x)＝，f′(0)＝1－a，因为函数f(x)在点(0，f(0))的切线与直线2x＋y－1＝0平行，所以1－a＝－2，a＝3.

(2)f′(x)＝，令f′(x)＝0，

当a＝0时，解得x＝1，在(0,1)上，

有f′(x)>0，函数f(x)单增；在(1,2)上，有f′(x)<0，函数f(x)单减，而f(0)＝0，f(2)＝，函数f(x)的最小值为0，结论不成立．

当a≠0，解得x1＝1，x2＝1－.

若a<0，f(0)＝a<0.结论不成立；

若0<a≤1，则1－≤0，在(0,1)上，有f′(x)>0，

函数f(x)单增；在(1,2) 上，有f′(x)<0，函数f(x)单减．只需得到所以≤a≤1；

若a>1,0<1－<1，在上，有f′(x)<0，函数f(x)单减；在上，有f′(x)>0，函数f(x)单增；在(1,2)上有f′(x)<0，函数f(x)单减．函数在x＝1－有极小值，只需得到

因为2a－1>1，e－1－<1，所以a>1.综上所述，a的取值范围是