题目内容
(理科做) 设函数
(1)若a>0,求函数 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,
求f (x)>b恒成立的概率
(1)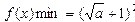
(2)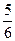
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
(理科做) 设函数
(1)若a>0,求函数 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,
求f (x)>b恒成立的概率
(1)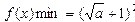
(2)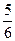
解析

 阅读快车系列答案
阅读快车系列答案