题目内容

6．若三直线2x+3y+8=0，x-y-1=0和x+ky=0相交于一点，则k=（　　）
A．-2B．$-\frac{1}{2}$C．2D．$\frac{1}{2}$

分析 通过前两个直线求出三直线的交点，然后代入第三条直线求k．

解答 解：因为三直线2x+3y+8=0，x-y-1=0和x+ky=0相交于一点，
所以解$\left\{\begin{array}{l}{2x+3y+8=0}\\{x-y-1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$，即交点为（-1，-2），
所以-1+（-2）k=0，解得k=$-\frac{1}{2}$；
故选B．

点评 本题考查了直线的交点以及点与直线的关系；属于基础题．

练习册系列答案
相关题目
16．曲线y=xex在点（1，e）处的切线与直线ax+by+c=0垂直，则$\frac{a}{b}$的值为$\frac{1}{2e}$．
17．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），F1、F2分别为它的左、右焦点，过焦点且垂直于X轴的弦长为3，且两焦点与短轴一端点构成等边三角形．
（1）求椭圆C的方程；
（2）问是否存在过椭圆焦点F2的弦PQ，使得|PF1|，|PQ|，|QF1|成等差数列，若存在，求出PQ所在直线方程；若不存在，请说明理由．
14．在△ABC中，B=30°，C=45°，则$\frac{a+c}{b}$=$\frac{\sqrt{6}+3\sqrt{2}}{2}$．
1．已知数列{an}满足a1=2，an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$（n∈N*），则连乘积a1a2a3…a2009a2010的值为（　　）
A．-6B．3C．2D．1
11．如图，在平面直角坐标系xOy中，已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点为F，点A，B在椭圆E上，直线AB经过坐标原点O．若AF⊥x轴，cos∠AFB=-$\frac{3}{5}$，则椭圆E的离心率e=$\frac{1}{2}$．
18．在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=12，BD=9，则此梯形的中位线长是（　　）
A．10B．$\frac{21}{2}$C．$\frac{15}{2}$D．12
15．在直角坐标系xoy中，曲线C1：$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t为参数，t≠0），其中0≤α＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，曲线C3：ρ=2$\sqrt{3}$cosθ．
（Ⅰ）求C2与C3交点的直角坐标；
（Ⅱ）若C2与C1相交于点A，C3与C1相交于点B，求|AB|的最大值．
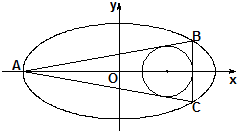16．如图，已知圆（x-2）2+y2=$\frac{4}{9}$是椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的内接△ABC的内切圆，其中A为椭圆C的左顶点，且椭圆C的离心率为$\frac{{\sqrt{15}}}{4}$，则此椭圆的标准方程为$\frac{x^2}{16}+{y^2}=1$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网