题目内容
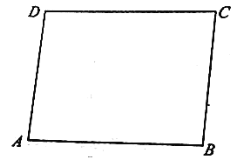
【题目】如图，矩形
是某生态农庄的一块植物栽培基地的平面图，现欲修一条笔直的小路
（宽度不计）经过该矩形区域，其中都在矩形的边界上.已知
，
（单位：百米），小路将矩形分成面积分别为
，
（单位：平方百米）的两部分，其中
，且点
在面积为的区域内，记小路的长为
百米.
（1）若
，求的最大值；
（2）若
，求的取值范围.
【答案】（1）
；（2）
【解析】
（1）
，故
得到答案.
（2）如图所示：折痕
有三种情况，依次计算每种情况
的取值范围，综合得到答案.
（1）如图所示：折痕有如下三种情况，易知图2图3不满足
，
如图1：，故
，
当
时等号成立，故，即
的最大值为；
（2）
，
，故
.
如图1：
，故
，
，
当
时，
，当
时，
，故
；
如图2：
，故
，
，
，故
；
如图3：
，故
，
，
，故
.
综上所述：
.
名师点拨卷系列答案【题目】某单位对员工业务进行考核，从
类员工(工作3年及3年以内的员工)和
类员工(工作3年以上的员工)的成绩中各抽取15个，具体数据如下：
类成绩：20 10 22 30 15 12 41 22 31 25 12 26 29 32 33
类成绩：21 40 30 41 42 31 49 51 52 43 47 47 32 45 48
（1）根据两组数据完成两类员工成绩的茎叶图，并通过茎叶图比较两类员工成绩的平均值及分散程度(不要求计算出具体值，得出结论即可)；
（2）研究发现从业时间与业务能力之间具有线性相关关系，从上述抽取的
名员工中抽取4名员工的成绩如下：
员工工作时间 | 1 | 2 | 3 | 4 |
考核成绩 | 10 | 15 | 20 | 30 |
根据四个的数据，求
关于
的线性回归方程．
附：回归直线
的斜率和截距的最小二乘法估计公式分别为：
，
．
【题目】中国大学先修课程，是在高中开设的具有大学水平的课程，旨在让学有余力的高中生早接受大学思维方式、学习方法的训练，为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年，两年共招收学生2000人，其中有300人参与学习先修课程，两年全校共有优等生200人，学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试，并且都参加了某高校的自主招生考试（满分100分），结果如下表所示：
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
（1）填写列联表，并画出列联表的等高条形图，并通过图形判断学习先修课程与优等生是否有关系，根据列联表的独立性检验，能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系？
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
（2）已知今年有150名学生报名学习大学先修课程，以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人，求他获得某高校自主招生通过的概率；
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为
，求
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式：
，其中
.
