题目内容
在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=9.
(1)判断两圆的位置关系;
(2)求直线m的方程,使直线m被圆C1截得的弦长为4,与圆C2截得的弦长是6.
(1)判断两圆的位置关系;
(2)求直线m的方程,使直线m被圆C1截得的弦长为4,与圆C2截得的弦长是6.
分析:(1)先根据两圆的方程求出这两个圆的圆心和半径,再根据两个圆的圆心距大于半径之和,可得两个圆相离.
(2)由题意得,所求的直线过两圆的圆心,即为连心线所在直线,用两点式求得得连心线所在直线方程.
(2)由题意得,所求的直线过两圆的圆心,即为连心线所在直线,用两点式求得得连心线所在直线方程.
解答:解:(1)由于圆C1的圆心C1(-3,1),半径r1=2;圆C2的圆心C2(4,5),半径r2=2.可得两圆的圆心距C1C2=
=
>r1+r2,
∴两圆相离.
(2)由题意得,所求的直线过两圆的圆心,即为连心线所在直线,
用两点式求得得连心线所在直线方程为:
=
,即 4x-7y+19=0.
| 72+42 |
| 65 |
∴两圆相离.
(2)由题意得,所求的直线过两圆的圆心,即为连心线所在直线,
用两点式求得得连心线所在直线方程为:
| y-1 |
| 5-1 |
| x+3 |
| 4+3 |
点评:本题主要考查两个圆的位置关系的判定方法,用两点式求直线的方程,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
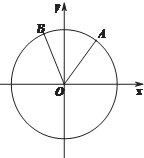 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是