题目内容
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].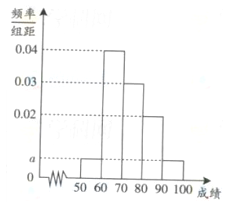
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
(1)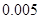 (2)75 (3)10人
(2)75 (3)10人
解析

练习册系列答案
相关题目
某电视台在一次对文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关数据如下表所示:
| | 文艺节目 | 新闻节目 | 总计 |
| 20岁到40岁 | 40 | 20 | 60 |
| 40岁以上 | 15 | 25 | 40 |
| 总计 | 55 | 45 | 100 |
(1)用分层抽样方法在收看新闻节目的观众中,随机抽取9名,那么40岁以上的观众应抽取几名?
(2)由表中数据分析,我们能否有99%的把握认为收看新闻节目的观众与年龄有关?(最后结果保留3位有效数字,四舍五入)
附:
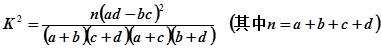
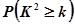 | 0.05 | 0.01 | 0.005 | 0.001 |
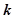 | 3.841 | 6.635 | 7.879 | 10.828 |
某学校高一年学生在某次数学单元测试中,成绩在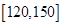 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 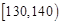 | 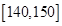 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
,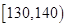 和
和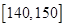 的同学中共抽取
的同学中共抽取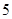 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
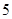 人中,任取
人中,任取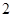 人,求成绩在
人,求成绩在 和
和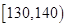 中各有
中各有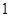 人的概率?
人的概率? 某工厂有工人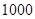 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外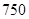 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 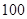 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 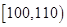 | 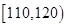 |  | 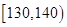 | 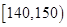 |
| 人数 | 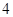 |  |  | 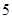 |  |
| 生产能力分组 | 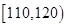 |  | 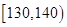 | 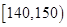 |
| 人数 |  |  |  |  |
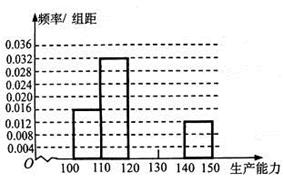
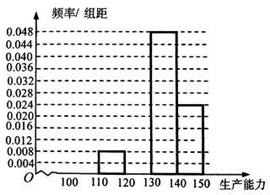
①求
 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;②分别估计
 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).

 ,
,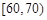 ,
, ,
,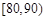 ,
,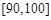 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
 ,
, ,
,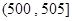 ,
, ,
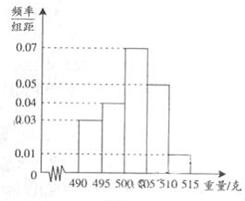
,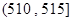 ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题: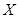 为合格产品的数量,求
为合格产品的数量,求 ;
; 


 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求