题目内容
甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的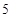 次预赛成绩记录如下:
次预赛成绩记录如下:
甲 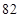
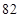

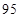
 乙
乙 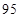

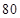

(1)用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)①求甲、乙两人的成绩的平均数与方差,②若现要从中选派一人参加数学竞赛,
根据你的计算结果,你认为选派哪位学生参加合适?
(1)详见解析;(2)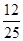 ;(3)①
;(3)① ,
,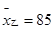 ;
;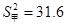 ,
,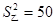 ;②甲的成绩较稳定,派甲参赛比较合适。
;②甲的成绩较稳定,派甲参赛比较合适。
解析试题分析:(1)十位数字为茎,个位数字为叶。(2)从甲、乙两人的成绩中各随机抽取一个用有序实数对表示,将所有情况一一例举出来,再将甲的成绩比乙高的事件一一例举出来,根据古典概型概率公式求其概率。(3)①根据平均数公式和方差公式可直接求得。②甲乙的平均数相同,但甲的方差小于乙的方差说明甲的成绩更稳定。
试题解析:解:(1)作出茎叶图如下; 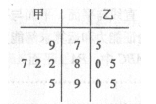 2分
2分
(2)记甲被抽到的成绩为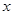 ,乙被抽到成绩为
,乙被抽到成绩为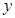 ,用数对
,用数对 表示基本事件:
表示基本事件: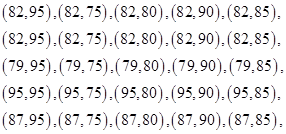
基本事件总数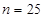 4分
4分
记“甲的成绩比乙高”为事件A,事件A包含的基本事件: 5分
5分
事件A包含的基本事件数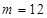 ,所以
,所以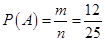
所以甲的成绩比乙高的概率为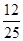 6分
6分
(3)①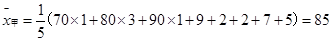 ,
,

 10分
10分
②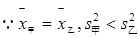 ,
, 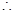 甲的成绩较稳定,派甲参赛比较合适。 12分
甲的成绩较稳定,派甲参赛比较合适。 12分
考点:1茎叶图;2古典概型概率;3平均数、方差。

 名校课堂系列答案
名校课堂系列答案某工厂有工人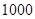 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外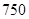 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 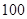 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 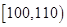 | 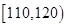 |  | 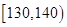 | 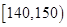 |
| 人数 | 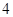 |  |  | 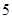 |  |
| 生产能力分组 | 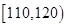 |  | 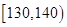 | 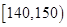 |
| 人数 |  |  |  |  |
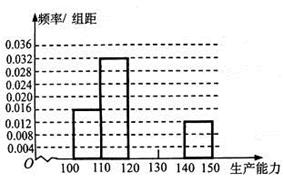
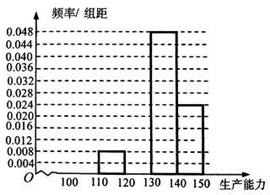
①求
 、
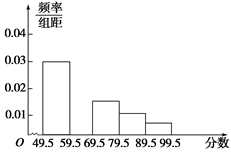
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;②分别估计
 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
| 0.6 | 1.2 | 2.7 | 1.5 | 2.8 | 1.8 | 2.2 | 2.3 | 3.2 | 3.5 |
| 2.5 | 2.6 | 1.2 | 2.7 | 1.5 | 2.9 | 3.0 | 3.1 | 2.3 | 2.4 |
| 3.2 | 1.7 | 1.9 | 0.8 | 0.9 | 2.4 | 1.2 | 2.6 | 1.3 | 1.4 |
| 1.6 | 0.5 | 1.8 | 0.6 | 2.1 | 1.1 | 2.5 | 1.2 | 2.7 | 0.5 |
(2) 根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
| A药 | | B药 |
| | 0. 1. 2. 3. | |
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 =bx+a.
=bx+a.(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
为了解某市民众对政府出台楼市限购令的情况,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令赞成的人数如下表:
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令?
| | 非高收入族 | 高收入族 | 合计 |
| 赞成 | | | |
| 不赞成 | | | |
| 合计 | | | |
附:K2=
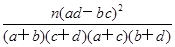
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
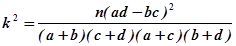 )其中n=a+b+c+d
)其中n=a+b+c+d 
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求