题目内容
已知数列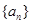 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意的
项和,对于任意的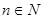 ,满足关系式
,满足关系式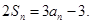
(1)求数列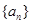 的通项公式;
的通项公式;
(2)设数列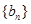 的通项公式是
的通项公式是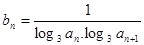 ,前
,前 项和为
项和为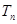 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有
(1)
(2)根据列项求和法来得到数列的前n项和 进而证明。
进而证明。
解析试题分析:
解:(1)由已知得
故 , 即
, 即
故数列 为等比数列,且
为等比数列,且
又当 时,
时,

而 亦适合上式
亦适合上式 
(2)
所以


考点:等比数列
点评:主要是考查了等比数列的通项公式和裂项法求和的综合运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
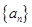 中,
中,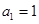 ,
,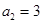 ,
, 对任意
对任意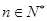 成立,令
成立,令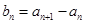 ,且
,且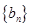 是等比数列.
是等比数列.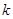 的值;
的值;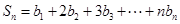 .
.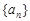 的前
的前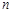 项和为
项和为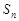 ,
,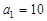 ,
, .
. 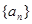 的通项公式;
的通项公式;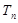 是数列
是数列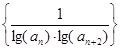 的前
的前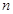 项和,求
项和,求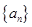 中,
中, ,
,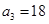 ,等差数列
,等差数列 中,
中, ,且
,且 。
。 ;(2)求数列
;(2)求数列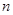 项和
项和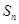 。
。 为等差数列
为等差数列 的前
的前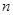 项和,
项和, ,
, ,求
,求 .
. 求首项
求首项 和公比
和公比 .
.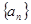 是各项为正数的等比数列,且a1=1,a2+a3=6,
是各项为正数的等比数列,且a1=1,a2+a3=6,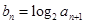 ,
,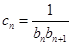 求该数列
求该数列 的前n项和
的前n项和
 的首项
的首项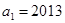 ,公比
,公比 ,数列
,数列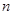 项的积记为
项的积记为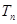 .
.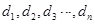 ,证明:数列
,证明:数列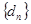 为等比数列.
为等比数列.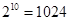 )
) 是等比数列,且
是等比数列,且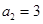 ,
,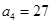
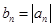 ,求
,求 的前
的前 项的和
项的和
 满足:
满足:
 为等比数列;
为等比数列; 为递增数列;
为递增数列; 的取值范围。
的取值范围。