题目内容
【题目】已知数列{an}满足,an+1=an+1![]() ,a1=a,则一定存在a,使数列中( )
,a1=a,则一定存在a,使数列中( )
A.存在n∈N*,有an+1an+2<0
B.存在n∈N*,有(an+1﹣1)(an+2﹣1)<0
C.存在n∈N*,有![]()
D.存在n∈N*,有![]()
【答案】C
【解析】
由函数![]() 与y=x有两个交点(0,0),(1,1),对a分类判断A,B错误;由a1>1时,a2一定小于
与y=x有两个交点(0,0),(1,1),对a分类判断A,B错误;由a1>1时,a2一定小于![]() ,则之后均小于
,则之后均小于![]() ,判断D错误;举例说明C正确.
,判断D错误;举例说明C正确.
因为an+1=an+1![]() ,
,
所以![]() 在函数
在函数![]() 图象上,
图象上,
因为![]() 与y=x有两个交点(0,0),(1,1),
与y=x有两个交点(0,0),(1,1),
如图所示:

可知当a1<0时,数列递减,∴an<0;
当0<a1<1时,数列递增,并且an趋向1;
当a1>1时,数列递减,并且an趋向1,则可知A,B错误;
又当x>1时,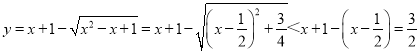 ,
,
则当a1>1时,a2一定小于![]() ,则之后均小于
,则之后均小于![]() ,∴D错误;
,∴D错误;
对于C,可取![]() ,得
,得![]() ,
,![]()
![]() ,
,
所以![]() ,满足要求.
,满足要求.
故选:C.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】2019年郑开国际马拉松比赛,于2019年3月31日在郑州、开封举行.某学校本着“我运动,我快乐,我锻炼,我提高”精神,积极组织学生参加比赛及相关活动,为了了解学生的参与情况,从全校学生中随机抽取了150名学生,对是否参与的情况进行了问卷调查,统计数据如下:
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
(1)根据上表说明,能否有97.5%的把握认为参与马拉松赛事与性别有关?
(2)现从参与问卷调查且参与赛事的学生中,采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动,
①求男、女学生各选取多少人;
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍,求恰好选到2名男生的概率.
附:参考公式:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |