题目内容
(本小题满分14分)
已知二次函数 ,关于
,关于 的不等式
的不等式 的解集为
的解集为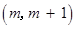 ,其中
,其中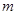 为非零常数.设
为非零常数.设 .
.
(1)求 的值;
的值;
(2) R
R 如何取值时,函数
如何取值时,函数

 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且
 ,求证:
,求证: N
N
(1)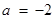 (2)当
(2)当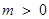 时,
时,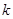 取任意实数, 函数
取任意实数, 函数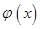 有极小值点
有极小值点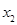 ;
;
当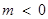 时,
时,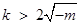 ,函数
,函数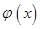 有极小值点
有极小值点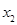 ,有极大值点
,有极大值点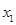 .
.
(其中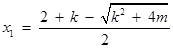 ,
, 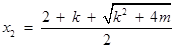 )
)
(3)① 当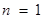 时,左边
时,左边 ,右边
,右边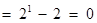 ,不等式成立;② 假设当
,不等式成立;② 假设当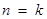
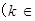 N
N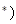 时,不等式成立,即
时,不等式成立,即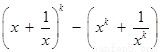
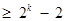 ,
,
则 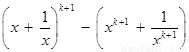
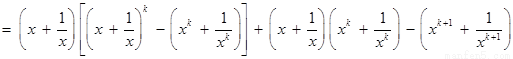
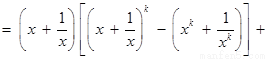
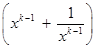
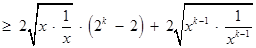
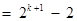 .
.
也就是说,当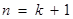 时,不等式也成立.
时,不等式也成立.
由①②可得,对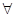
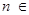 N
N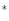 ,
,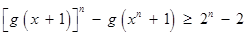 都成立.
都成立.
【解析】
试题分析:(1)解:∵关于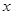 的不等式
的不等式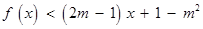 的解集为
的解集为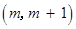 ,
,
即不等式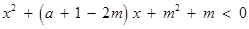 的解集为
的解集为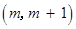 ,
,
∴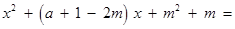
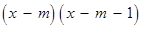 .
.
∴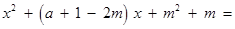
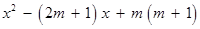 .
.
∴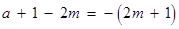 .
.
∴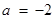 .
.
(2)解法1:由(1)得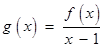
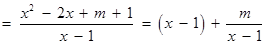 .
.
∴
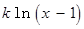
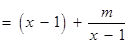
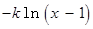 的定义域为
的定义域为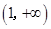 .
.
∴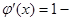
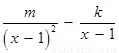
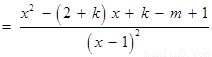 .
.
方程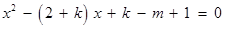 (*)的判别式
(*)的判别式
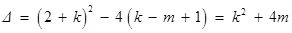 .
.
①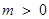 时,
时,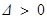 ,方程(*)的两个实根为
,方程(*)的两个实根为

则 时,
时,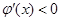 ;
;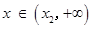 时,
时,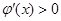 .
.
∴函数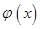 在
在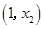 上单调递减,在
上单调递减,在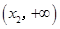 上单调递增.
上单调递增.
∴函数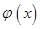 有极小值点
有极小值点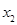 .
.
②当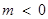 时,由
时,由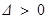 ,得
,得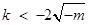 或
或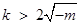 ,
,
若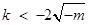 ,则
,则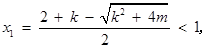
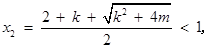
故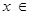
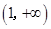 时,
时,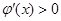 ,
,
∴函数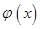 在
在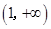 上单调递增.
上单调递增.
∴函数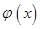 没有极值点.
没有极值点.
若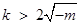 时,
时,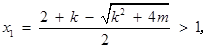
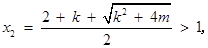
则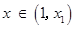 时,
时,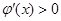 ;
;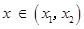 时,
时,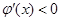 ;
;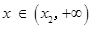 时,
时,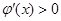 .
.
∴函数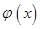 在
在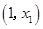 上单调递增,在
上单调递增,在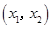 上单调递减,在
上单调递减,在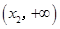 上单调递增.
上单调递增.
∴函数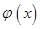 有极小值点
有极小值点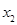 ,有极大值点
,有极大值点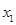 .
.
综上所述, 当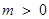 时,
时,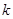 取任意实数, 函数
取任意实数, 函数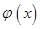 有极小值点
有极小值点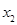 ;
;
当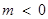 时,
时,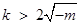 ,函数
,函数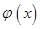 有极小值点
有极小值点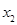 ,有极大值点
,有极大值点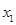 .
.
(其中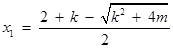 ,
, 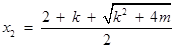 )
)
解法2:由(1)得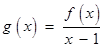
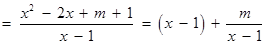 .
.
∴
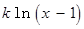
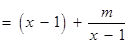
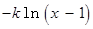 的定义域为
的定义域为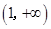 .
.
∴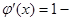
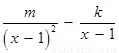
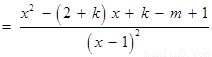 .
.
若函数
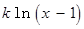 存在极值点等价于函数
存在极值点等价于函数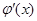 有两个不等的零点,且
有两个不等的零点,且
至少有一个零点在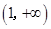 上.
上.
令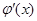
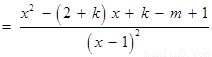
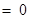 ,
,
得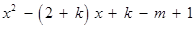
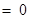 ,
(*)
,
(*)
则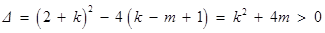 ,(**)
,(**)
方程(*)的两个实根为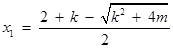 ,
, 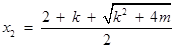 .
.
设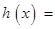
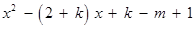 ,
,
①若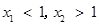 ,则
,则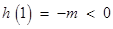 ,得
,得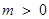 ,此时,
,此时,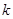 取任意实数, (**)成立.
取任意实数, (**)成立.
则 时,
时,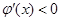 ;
;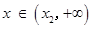 时,
时,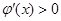 .
.
∴函数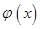 在
在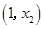 上单调递减,在
上单调递减,在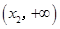 上单调递增.
上单调递增.
∴函数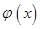 有极小值点
有极小值点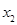 .
.
②若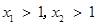 ,则
,则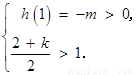 得
得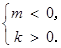
又由(**)解得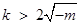 或
或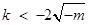 ,
,
故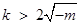 .
.
则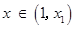 时,
时,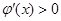 ;
;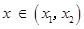 时,
时,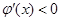 ;
;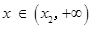 时,
时,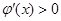 .
.
∴函数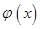 在
在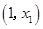 上单调递增,在
上单调递增,在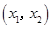 上单调递减,在
上单调递减,在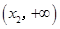 上单调递增.
上单调递增.
∴函数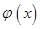 有极小值点
有极小值点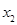 ,有极大值点
,有极大值点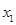 .
.
综上所述, 当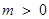 时,
时,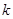 取任何实数, 函数
取任何实数, 函数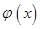 有极小值点
有极小值点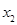 ;
;
当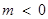 时,
时,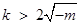 ,函数
,函数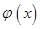 有极小值点
有极小值点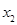 ,有极大值点
,有极大值点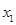
(其中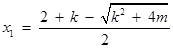 ,
, 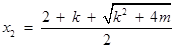 )
)
(2)证法1:∵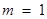 , ∴
, ∴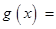
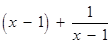 .
.
∴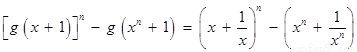

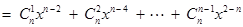 .
.
令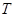
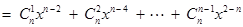 ,
,
则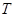
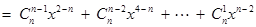
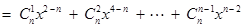 .
.
∵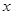
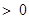 ,
,
∴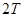
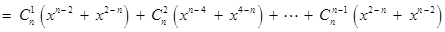
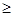
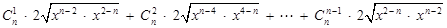
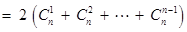

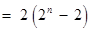 .
.
∴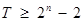 ,即
,即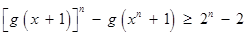 .
.
证法2:下面用数学归纳法证明不等式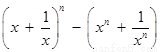
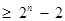 .
.
① 当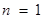 时,左边
时,左边 ,右边
,右边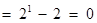 ,不等式成立;
,不等式成立;
② 假设当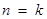
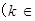 N
N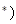 时,不等式成立,即
时,不等式成立,即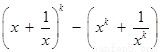
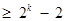 ,
,
则 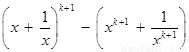
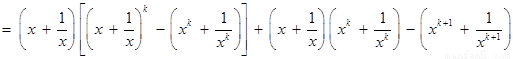
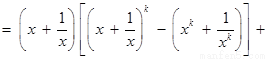
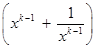
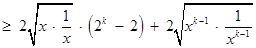
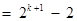 .
.
也就是说,当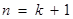 时,不等式也成立.
时,不等式也成立.
由①②可得,对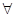
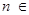 N
N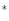 ,
,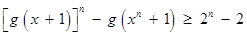 都成立.
都成立.
考点:本小题主要考查二次函数、一元二次不等式、一元二次方程、函数应用、均值不等式等基础知识
点评:本题计算量大,第二问中要对参数分情况讨论再次加大了试题的难度,第三问数学归纳法用来证明和正整数有关的题目。本题还考查了数形结合、函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)