题目内容
3.已知椭圆的中心为原点O,长轴的左右端点分别为A、B、F为椭圆的左焦点,离心率e=$\frac{\sqrt{2}}{2}$,且$\overrightarrow{AF}$•$\overrightarrow{FB}$=1.(1)求椭圆的标准方程;
(2)若D、E是抛物线y2=-8x的准线上的两个动点,且|DE|=4,设△DEF的内切圆圆心C的坐标为(x,y)
①求△DEF的周长l关于x、y的表达式;
②求点C的轨迹方程.
分析 (1)利用$\overrightarrow{AF}$•$\overrightarrow{FB}$=1及$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,计算即得结论;
(2)由题意易得:圆心C(x,y)、半径r=2-x、FC=$\sqrt{(x+1)^{2}+{y}^{2}}$.
①通过内切圆的性质及勾股定理可得FU=FV=$\sqrt{6x+{y}^{2}-3}$,利用等量代换可得△DEF的周长l=8+2$\sqrt{6x+{y}^{2}-3}$;②利用面积的不同计算方法计算即得结论.
解答 解:(1)由题意可知:A(-a,0),B(a,0),F(-c,0),
∵$\overrightarrow{AF}$•$\overrightarrow{FB}$=1,∴(a-c,0)•(a+c,0)=a2-c2=1,
又∵e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{2}$,
∴a2=2,c2=1,∴b2=a2-c2=1,
∴椭圆的标准方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)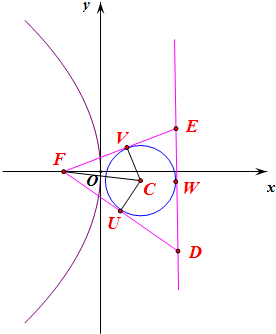 由题意,圆心C(x,y),∴FC=$\sqrt{(x+1)^{2}+{y}^{2}}$,
由题意,圆心C(x,y),∴FC=$\sqrt{(x+1)^{2}+{y}^{2}}$,
∵D、E是抛物线y2=-8x的准线上的两个动点,
∴DE所在的直线为x=2,
∴圆C半径r=2-x,内切圆C与△DEF各边的切点如图所示.
①FU=FV=$\sqrt{F{C}^{2}-V{C}^{2}}$=$\sqrt{[(x+1)^{2}+{y}^{2}]-(2-x)^{2}}$=$\sqrt{6x+{y}^{2}-3}$,
∵|DE|=4,∴VE+DU=EW+DW=DE=4,
∴△DEF的周长为FD+DE+EF=2FU+2ED=2$\sqrt{6x+{y}^{2}-3}$+8,
即l=8+2$\sqrt{6x+{y}^{2}-3}$;
②由①可知△DEF的周长l=2$\sqrt{6x+{y}^{2}-3}$+8,
又∵S△DEF=$\frac{1}{2}•EF•r$+$\frac{1}{2}•DE•r$+$\frac{1}{2}•DF•r$=$\frac{1}{2}•l•r$,
∴S△DEF=$\frac{1}{2}•$(8+2$\sqrt{6x+{y}^{2}-3}$)•(2-x),
又∵S△DEF=$\frac{1}{2}•DE•(2+1)$=6,
∴$\frac{1}{2}•$(8+2$\sqrt{6x+{y}^{2}-3}$)•(2-x)=6,
化简得:6x3-43x2+52x-16+(x-2)2y2=0.
点评 本题是一道直线与圆锥曲线的综合题,考查椭圆的标准方程、直线与椭圆的位置关系、直线与圆的位置关系、三角形的周长与面积的计算等基础知识,考查运算求解能力,注意解题方法的积累,属于难题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | $\frac{1}{2n+1}$ | B. | $\frac{2n+2}{2n+1}$ | C. | $\frac{2n}{2n+1}$ | D. | $\frac{n}{2n+1}$ |
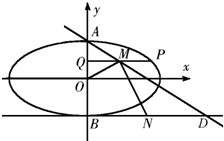 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.