题目内容
设关于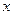 的函数
的函数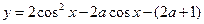 的最小值为
的最小值为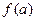 ,试确定满足
,试确定满足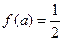 的
的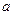 的值,并对此时的
的值,并对此时的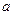 值求
值求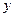 的最大值。
的最大值。
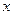 的函数
的函数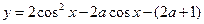 的最小值为
的最小值为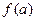 ,试确定满足
,试确定满足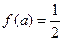 的
的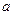 的值,并对此时的
的值,并对此时的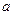 值求
值求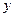 的最大值。
的最大值。见解析
解:令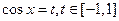 ,则
,则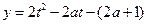 ,对称轴
,对称轴 ,
,
当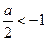 ,即
,即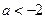 时,
时,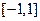 是函数
是函数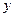 的递增区间,
的递增区间,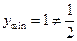 ;
;
当 ,即
,即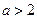 时,
时,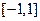 是函数
是函数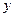 的递减区间,
的递减区间,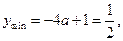 得
得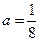 ,与
,与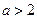 矛盾;
矛盾;
当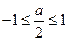 ,即
,即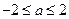 时,
时,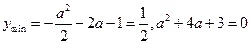 ,得
,得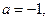 或
或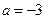 ,
,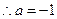 ,此时
,此时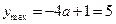 。
。
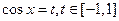 ,则
,则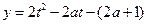 ,对称轴
,对称轴 ,
,当
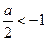 ,即
,即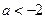 时,
时,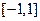 是函数
是函数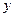 的递增区间,
的递增区间,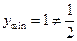 ;
;当
 ,即
,即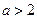 时,
时,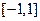 是函数
是函数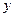 的递减区间,
的递减区间,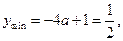 得
得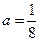 ,与
,与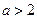 矛盾;
矛盾;当
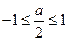 ,即
,即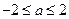 时,
时,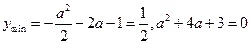 ,得
,得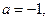 或
或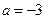 ,
,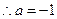 ,此时
,此时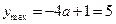 。
。
练习册系列答案
相关题目
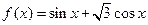
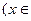 R
R .
.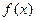 的最小正周期;
的最小正周期;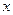 的值.
的值.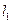 、
、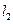 、
、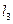 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.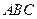 的三顶点分别放在
的三顶点分别放在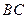 和
和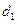 ,
,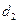 ,求
,求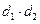 的范围?
的范围?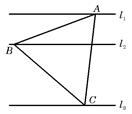
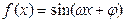
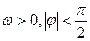 ),
),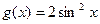 .若函数
.若函数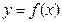 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为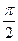 ,且直线
,且直线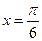 是函数
是函数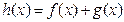 的单调递增区间.
的单调递增区间.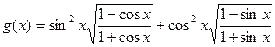 ,其中
,其中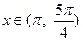 ,求函数
,求函数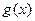 的值域.
的值域.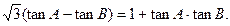
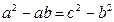 ,求A、B、C的大小;
,求A、B、C的大小;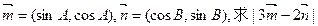 的取值范围.
的取值范围. 和
和 的终边关于y轴对称,则下列各式中正确的是
的终边关于y轴对称,则下列各式中正确的是 -
-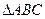 是锐角三角形,
是锐角三角形,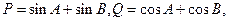 则( )
则( )
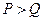

 与
与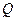 的大小不能确定
的大小不能确定