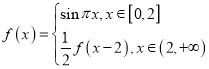题目内容
【题目】设函数![]() ,
,![]() .
.
(1)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求a,b的值;
处具有公共切线,求a,b的值;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围;
内恰有两个零点,求a的取值范围;
(3)![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)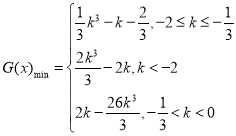
【解析】
(1)由题意求出![]() 由题意得
由题意得![]() ,且
,且![]() 解该方程组即可求出
解该方程组即可求出![]() 的值;(2)把
的值;(2)把![]() 代入
代入![]() 化简,并求出
化简,并求出![]() ,利用导数求出单调性和极值,由函数在
,利用导数求出单调性和极值,由函数在![]() 内有两零点列出不等式组,求出不等式的解集可得
内有两零点列出不等式组,求出不等式的解集可得![]() 的取值范围.
的取值范围.
(3)表示出![]() ,并求出
,并求出![]() ,利用导数求出单调性和极值点,按照在区间
,利用导数求出单调性和极值点,按照在区间![]() 内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最小值.
内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最小值.
(1)![]() ,
,![]() ,
,
![]() 由线
由线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,
处具有公共切线,
![]() ,
,![]() ,
,
即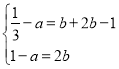 ,
,
解得![]() .
.
(2)![]() ,
,
![]() ,
,
![]()
![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
|
|
|
|
|
|
| |
|
| 极小值 |
|
![]() 在
在![]() 内恰有2个零点,
内恰有2个零点,
 ,即
,即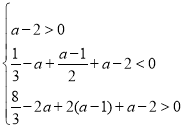 ,
,
解得![]() ,
,
因此a的取值范围是![]() .
.
(3)![]()
![]()
![]()
![]()
令![]() ,解得
,解得![]() ,
,
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 极大值 |
| 极小值 |
|
①当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 和
和![]() 单调递增,
单调递增,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
②![]() ,即
,即![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() .
.
③![]() ,即
,即![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() 在
在![]() 单调递增,
单调递增,
![]() .
.
综上所述,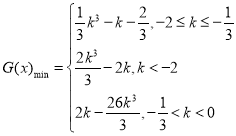 .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目