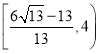题目内容
【题目】已知函数
，其中
，
为自然对数的底数.
（1）若函数
既有极大值又有极小值，试求实数
的取值范围；
（2）设
，且
，
是函数的两个零点，求证：
.
【答案】（1）
，
，
；（2）证明见解析.
【解析】
（1）求出
，令
，求出方程有两个不相等的根所满足的条件，即可求出结论；
（2）根据已知条件，求出
单调区间，得到
是极值点，不妨设
，将问题转化为证明
，即证
，结合单调性，只需证
，再由
，即证
，构造函数
，只需证明
，即可得证结论.
（1）
，
既有极大值又有极小值，
有两个不相等的实数根，即
且
.
由
且
，得
，，；
（2）证明：由（1）知，当
时，在
上单调递增，
在
上单调递减.又
，
令，则
.
，
在区间上单调递增，
.
.
，
是函数的两个零点，
不妨设，
，
，
，且在上单调递增，
，即.
由（1）可知，
.
练习册系列答案
相关题目
【题目】据统计，仅在北京地区每天就有500万单快递等待派送，近5万多名快递员奔跑在一线，快递网点人员流动性也较强，各快递公司需要经常招聘快递员，保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表：
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为：甲公司规定底薪
元，每单抽成
元；乙公司规定底薪
元，每日前
单无抽成，超过单的部分每单抽成
元．
（1）分别求甲、乙快递公司的快递员的日工资
（单位：元）与送货单数
的函数关系式；
（2）若将频率视为概率，回答下列问题：
①记甲快递公司的快递员的日工资为
（单位：元），求的分布列和数学期望；
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由．
