题目内容
已知实数a，b满足(
)a=(
)b，给出下列五个关系式：①0＜b＜a；②a＜b＜0；③0＜a＜b；④b＜a＜0；⑤a=b．其中能使得上式成立的个数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
分析：作出函数y=(
)x和y=（
）x的图象，利用数形结合即可得到结论．
| 1 |
| 2 |
| 1 |
| 3 |
解答：解：分别作出函数y=(
)x和y=（
）x的图象，如图，
由图象可知，若(
)a=(
)b，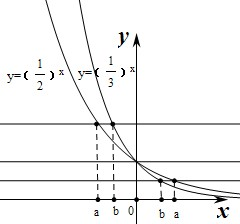
则当(
)a=(
)b＞0时，满足0＜b＜a，∴①正确．
当(
)a=(
)b=0时，满足a=b=0，∴⑤正确．
当(
)a=(
)b＜0时，满足条件a＜b＜0，∴②正确，
故正确的是①②⑤．
故选：C．
| 1 |
| 2 |
| 1 |
| 3 |
由图象可知，若(
| 1 |
| 2 |
| 1 |
| 3 |
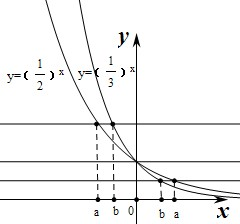
则当(
| 1 |
| 2 |
| 1 |
| 3 |
当(
| 1 |
| 2 |
| 1 |
| 3 |
当(
| 1 |
| 2 |
| 1 |
| 3 |
故正确的是①②⑤．
故选：C．
点评：本题主要考查指数函数的图象和性质，利用数形结合是解决本题的关键．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知实数a、b满足条件：ab＜0，且1是a2与b2的等比中项，又是
，
的等差中项，则
的值是（ ）
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|