题目内容
已知实数a、b满足条件:ab<0,且1是a2与b2的等比中项,又是
,
的等差中项,则
的值是( )
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
分析:根据等比数列与等差数列的性质可得a2b2=1,
+
=
=2,并且计算出ab=-1,a+b=-2.进而可得
=
=-
.
| 1 |
| a |
| 1 |
| b |
| a+b |
| ab |
| a+b |
| a2+b2 |
| a+b |
| (a+b)2-2ab |
| 1 |
| 3 |
解答:解:由题意得:1是a2与b2的等比中项,又是
,
的等差中项,
所以a2b2=1,
+
=
=2.
因为ab<0,
所以ab=-1,a+b=-2.
所以
=
=
=-
.
故选D.
| 1 |
| a |
| 1 |
| b |
所以a2b2=1,
| 1 |
| a |
| 1 |
| b |
| a+b |
| ab |
因为ab<0,
所以ab=-1,a+b=-2.
所以
| a+b |
| a2+b2 |
| a+b |
| (a+b)2-2ab |
| -2 |
| 4+2 |
| 1 |
| 3 |
故选D.
点评:解决此类问题的关键是数列掌握等差数列与等比数列的性质,并且把所求的式子进行正确的化简.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
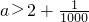 ;
; (x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是
(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,经过其中任意两点作直线,则不同直线的条数是