题目内容
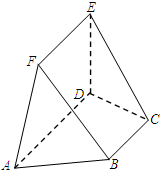
如图,在五面体 中,已知
中,已知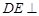 平面
平面 ,
,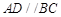 ,
,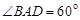 ,
,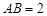 ,
,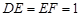 .
.
(1)求证: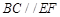 ;
;
(2)求三棱锥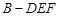 的体积.
的体积.
(1)详见解析,(2)
解析试题分析:(1)证明线线平行,一般思路为利用线面平行的性质定理与判定定理进行转化. 因为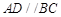 ,
,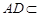 平面
平面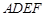 ,
,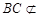 平面
平面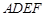 ,所以
,所以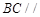 平面
平面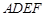 ,又
,又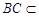 平面
平面 ,平面
,平面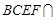 平面
平面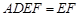 ,所以
,所以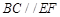 .(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为
.(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为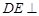 平面
平面 ,所以有面
,所以有面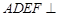 平面
平面 ,则作
,则作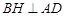 就可得
就可得 平面
平面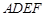 .证明
.证明 平面
平面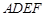 过程也可从线线垂直证线面垂直.确定
过程也可从线线垂直证线面垂直.确定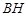 是三棱锥
是三棱锥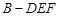 的高之后,可利用三棱锥
的高之后,可利用三棱锥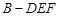 的体积公式
的体积公式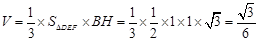 .
.
试题解析: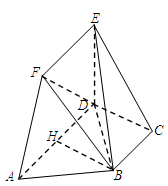
(1)因为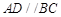 ,
,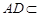 平面
平面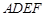 ,
,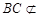 平面
平面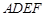 ,
,
所以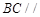 平面
平面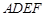 , 3分
, 3分
又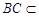 平面
平面 ,平面
,平面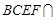 平面
平面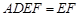 ,
,
所以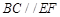 . 6分
. 6分
(2)在平面 内作
内作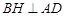 于点
于点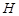 ,
,
因为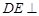 平面
平面 ,
,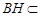 平面
平面 ,所以
,所以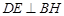 ,
,
又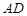 ,
,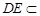 平面
平面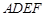 ,
,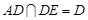 ,
,
所以 平面
平面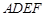 ,
,
所以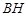 是三棱锥
是三棱锥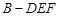 的高. 9分
的高. 9分
在直角三角形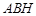 中,
中,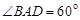 ,
,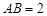 ,所以
,所以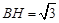 ,
,
因为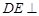 平面
平面 ,
,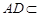 平面
平面 ,所以
,所以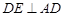 ,
,
又由(1)知,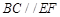 ,且
,且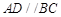 ,所以
,所以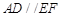

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
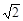 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.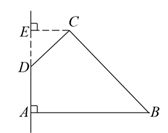
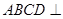 平面
平面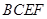 ,且四边形
,且四边形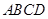 为矩形,四边形
为矩形,四边形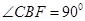 ,
,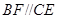 ,
,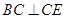 ,
,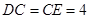 ,
,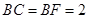 .
.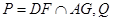 是直线
是直线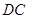 上的动点,判断并证明直线
上的动点,判断并证明直线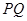 与直线
与直线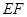 的位置关系.
的位置关系. 所成角的余弦值.
所成角的余弦值.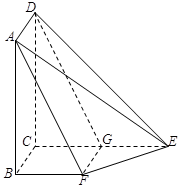
 中,
中, °,
°, ,
, 平面
平面 ,
, ,设
,设 的中点为
的中点为 ,
, .
.
 平面
平面 ;
; 的体积.
的体积. .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.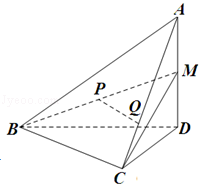

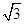 的正三棱锥
的正三棱锥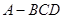 中,
中,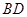 长为
长为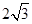 ,
,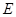 为棱
为棱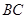 的中点,求
的中点,求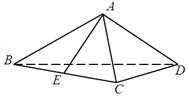
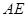 与
与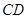 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
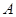 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点 AC
AC
 ABC体积的最大值.
ABC体积的最大值.