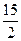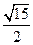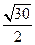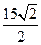题目内容
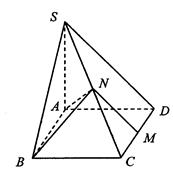
如图所示，已知四棱锥S—ABCD的底面ABCD是矩形，M、N分别是CD、SC的中点，SA⊥底面ABCD，SA=AD=1，AB=
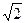.（1）求证：MN⊥平面ABN；
（2）求二面角A—BN—C的余弦值.
|
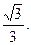
以A点为原点，AB为x轴，AD为y轴，
AD为z轴的空间直角坐标系，
则依题意可知相关各点的坐标分别是
A（0，0，0），B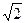（，0，0），C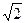（，1，0），D（0，1，0），S（0，0，1）
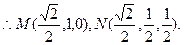
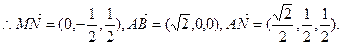
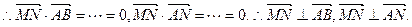
∴MN⊥平面ABN.
（2）设平面NBC的法向量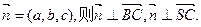
且又易知
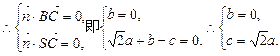
令a=1，则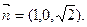
显然，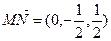
就是平面ABN的法向量.
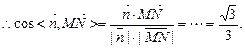
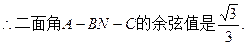
AD为z轴的空间直角坐标系，
则依题意可知相关各点的坐标分别是
A（0，0，0），B（
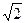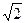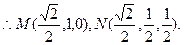
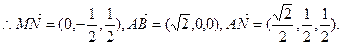
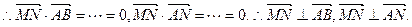
，0，0），C（，1，0），D（0，1，0），S（0，0，1）∴MN⊥平面ABN.
（2）设平面NBC的法向量
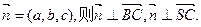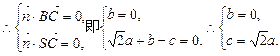
且又易知令a=1，则
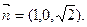
显然，
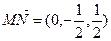就是平面ABN的法向量.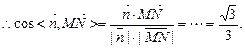
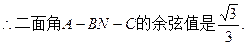
练习册系列答案
发散思维新课堂系列答案
相关题目
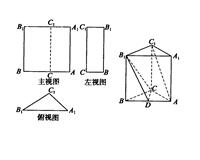
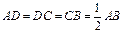，E是AB的中点，将△ADE沿DE折起，使点A折到点P的位置，且二面角
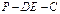的大小为1200．
；
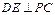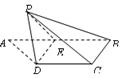
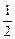，那么点M到直线EF的距离为( )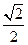
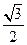
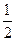
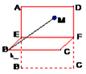
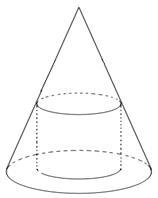
cm的内接圆柱. 
