题目内容
设函数y=f(x)在区间D上的导函数为f′(x),f′(x)在区间D上的导函数为g(x)。若在区间D上,g(x)<0恒成立,则称函数f(x)在区间D上为“凸函数”。已知实数m是常数, ,
,
(Ⅰ)若y=f(x)在区间[0,3]上为“凸函数”,求m的取值范围;
(Ⅱ)若对满足|m|≤2的任何一个实数m,函数f(x)在区间(a,b)上都为“凸函数”,求b-a的最大值。
 ,
,(Ⅰ)若y=f(x)在区间[0,3]上为“凸函数”,求m的取值范围;
(Ⅱ)若对满足|m|≤2的任何一个实数m,函数f(x)在区间(a,b)上都为“凸函数”,求b-a的最大值。
解:由函数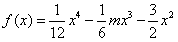 ,得
,得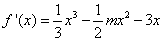 ,
,
∴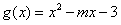 ,
,
(Ⅰ)若y=f(x)在区间[0,3]上为“凸函数”,则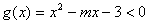 在区间[0,3]上恒成立,
在区间[0,3]上恒成立,
∵x=0时,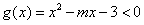 恒成立,
恒成立,
0<x≤3时,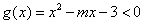 恒成立等价于
恒成立等价于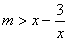 恒成立,
恒成立,
∵0<x≤3时,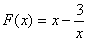 时增函数,
时增函数,
∴m>F(3),即m>2,
∴若f(x)在区间[0,3]上为“凸函数”,则m>2。
(Ⅱ)当|m|≤2时,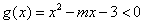 恒成立,
恒成立, |m|≤2时,
|m|≤2时,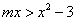 恒成立,
恒成立,
当x=0时,-3<0显然成立,
∵m的最小值是-2,
∴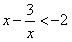 ,解得0<x<1,
,解得0<x<1,
当x<0,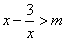 ,
,
∵m的最大值是2,
∴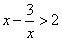 ,解得-1<x<0;
,解得-1<x<0;
综上可得-1<x<1,从而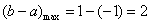 ,
,
∴b-a的最大值等于2。

练习册系列答案
相关题目
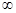 ,
,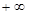 )内有定义,对于给定的正数k,定义函数:
)内有定义,对于给定的正数k,定义函数: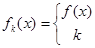
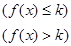 ,取函数
,取函数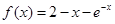 ,若对任意的x∈(-
,若对任意的x∈(-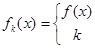
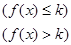 ,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+
∞),恒有fk(x)=f(x),则( )
,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+
∞),恒有fk(x)=f(x),则( )