题目内容
设函数y=f(x)在区间(a,b)上的导函数为f′(x),f′(x)在区间(a,b)上的导函数为
(x),若区间(a,b)上(x)<0恒成立,则称函数f(x)在区间(a,b)上的“凸函数”.已知f(x)=
x4-
mx3-
x2,若对任意的实数m满足|m|≤2时,函
数f(x)在区间(a,b)上的“凸函数”,则b-a最大值为( )
A.4 B.3 C.2 D.1
A.因为f′(x)=
x3-
mx2-3x,
所以(x)=x2-mx-3,
又Δ=m2+12>0恒成立,
设x2-mx-3=0的两根为x1,x2,
若x1<x2,
所以(x)<0,则x1<x<x2,
故(b-a)max=x2-x1
=
=
,
又-2≤m≤2,
所以(b-a)max=
=4.
练习册系列答案
相关题目
,
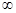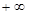)内有定义，对于给定的正数k，定义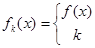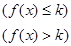函数：
,取函数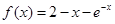
，若对任意的x∈(－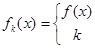
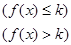,取函数f(x)=2-x-e-x，若对任意的x∈(-∞,+
∞)，恒有fk(x)＝f(x)，则( )