题目内容
设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数k,定义函数: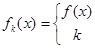
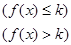 ,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+
∞),恒有fk(x)=f(x),则( )
,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+
∞),恒有fk(x)=f(x),则( )
A. k的最大值为2 B. k的最小值为2
C. k的最大值为1 D. k的最小值为1
【答案】
D
【解析】
试题分析:对函数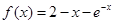 求导得
求导得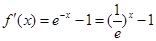 ,
,
当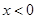 时,
时,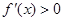 ,此时
,此时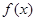 在
在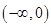 是增函数,
是增函数,
当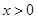 时,
时,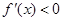 ,此时
,此时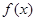 在
在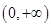 是减函数,
是减函数,
综上知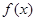 在
在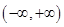 上有最大值
上有最大值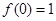 ,
,
要使得对任意的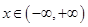 ,恒有
,恒有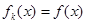 ,则可知
,则可知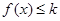 恒成立,所以只要找到
恒成立,所以只要找到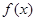 的最大值即可,所以
的最大值即可,所以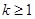 ,所以k的最小值是1.
,所以k的最小值是1.
考点:函数的单调性与导数的关系,恒成立问题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
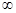 ,
,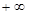 )内有定义,对于给定的正数k,定义函数:
)内有定义,对于给定的正数k,定义函数: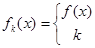
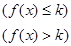 ,取函数
,取函数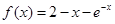 ,若对任意的x∈(-
,若对任意的x∈(-