题目内容
(本小题满分12分)
如右图,四边形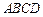 是圆柱
是圆柱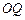 的轴截面,点
的轴截面,点 在圆柱
在圆柱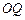 的底面圆周上,
的底面圆周上,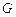 是
是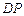 的中点,圆柱
的中点,圆柱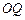 的底面圆的半径
的底面圆的半径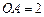 ,侧面积为
,侧面积为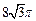 ,
,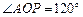 .
.
(Ⅰ)求证: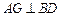 ;
;
(Ⅱ)求二面角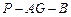 的平面角的余弦值.
的平面角的余弦值.
如右图,四边形
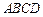 是圆柱
是圆柱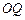 的轴截面,点
的轴截面,点 在圆柱
在圆柱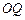 的底面圆周上,
的底面圆周上,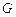 是
是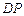 的中点,圆柱
的中点,圆柱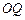 的底面圆的半径
的底面圆的半径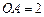 ,侧面积为
,侧面积为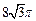 ,
,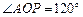 .
.(Ⅰ)求证:
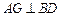 ;
;(Ⅱ)求二面角
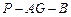 的平面角的余弦值.
的平面角的余弦值.
解:(1)(解法一):由题意可知  ,解得
,解得  ,
,
在 中,
中, , ∴
, ∴  ,
,
又 ∵ 是
是 的中点,∴
的中点,∴  .① ∵
.① ∵  为圆
为圆 的直径,∴
的直径,∴  .
.
由已知知 ,∴
,∴  ,∴
,∴  .
.
∴ . ②∴ 由①②可知:
. ②∴ 由①②可知: ,∴
,∴  .
.
(2) 由(1)知: , ∴
, ∴ ,
, ,
,
∴ 是二面角
是二面角 的平面角 .
的平面角 .  ,
,  ,
,  .
.

∴ .
.  .
.
(解法二):建立如图所示的直角坐标系,
由题意可知 .解得
.解得 .
.
则 ,
, ,
, ,
, , ∵
, ∵ 是
是 的中点,∴ 可求得
的中点,∴ 可求得 .
.
(1) ,
, ,∴
,∴  . ∵
. ∵ ,∴
,∴  .
.
(2)由(1)知, ,
,  ,
, ,
,  .
.
∵ ,
, ∴
∴ 是平面
是平面 的法向量.
的法向量.
设 是平面
是平面 的法向量,由
的法向量,由 ,
, ,解得
,解得
 . 所以二面角
. 所以二面角 的平面角的余弦值
的平面角的余弦值 .
.
 ,解得
,解得  ,
, 在
 中,
中, , ∴
, ∴  ,
,又 ∵
 是
是 的中点,∴
的中点,∴  .① ∵
.① ∵  为圆
为圆 的直径,∴
的直径,∴  .
.由已知知
 ,∴
,∴  ,∴
,∴  .
. ∴
 . ②∴ 由①②可知:
. ②∴ 由①②可知: ,∴
,∴  .
. (2) 由(1)知:
 , ∴
, ∴ ,
, ,
,∴
 是二面角
是二面角 的平面角 .
的平面角 .  ,
,  ,
,  .
.
∴
 .
.  .
. (解法二):建立如图所示的直角坐标系,
由题意可知
 .解得
.解得 .
. 则
 ,
, ,
, ,
, , ∵
, ∵ 是
是 的中点,∴ 可求得
的中点,∴ 可求得 .
. (1)
 ,
, ,∴
,∴  . ∵
. ∵ ,∴
,∴  .
. (2)由(1)知,
 ,
,  ,
, ,
,  .
. ∵
 ,
, ∴
∴ 是平面
是平面 的法向量.
的法向量. 设
 是平面
是平面 的法向量,由
的法向量,由 ,
, ,解得
,解得
 . 所以二面角
. 所以二面角 的平面角的余弦值
的平面角的余弦值 .
. 略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
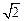 .
.
 的直观图与三视图如图所示
的直观图与三视图如图所示 积;
积;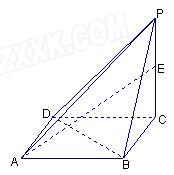

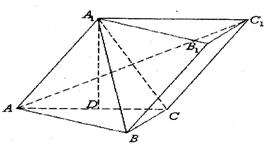
 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,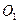 是
是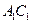 和
和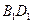 的交点。
的交点。
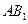 与底面
与底面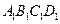 所成的角的大小为
所成的角的大小为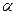 ,二面角
,二面角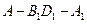 的大小为
的大小为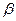 。
。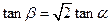 ;
;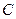 到平面
到平面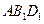 的距离为
的距离为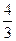 ,求正四棱柱
,求正四棱柱 B
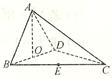
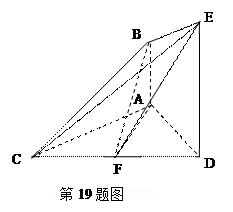
B 分别为棱AC、AB上的动点(不包括端点),若
分别为棱AC、AB上的动点(不包括端点),若

 则线段DE长度的取值范围为
则线段DE长度的取值范围为 B.
B. C.
C. D.
D.
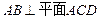 ,
,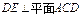 ,
,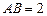 ,
,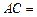
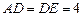 ,
,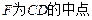 .
.
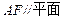
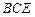 ;
; 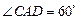 ,求二面角
,求二面角 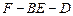 的余弦值.
的余弦值.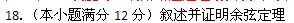
 ,
, ,
,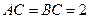 ,
,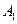 在底面
在底面 上的射影恰为
上的射影恰为 的中点
的中点 ,又知
,又知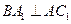 .
. ;
; 到平面
到平面 的距离;
的距离; .
.
 的外接球球心在
的外接球球心在 上,且
上,且 ,
, ,在外接球面上
,在外接球面上 两点
两点 间的球面距离是 。
间的球面距离是 。